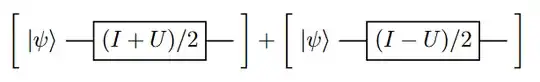Realization of the gate $(I\pm U)/2$

Question

The state after applying the Hadamard test (before measurement)

is $$\newcommand{\ket}[1]{|#1\rangle}\newcommand{\bra}[1]{\langle#1|}\ket{0}\frac{I+U}{2}\ket{\psi} + \ket{1}\frac{I-U}{2}\ket{\psi}.$$

Therefore, the density matrix of $\ket{\psi'}$ is:

$$\rho = \left(\frac{I+U}{2}\right)\ket{\psi}\bra{\psi}\left(\frac{I+U}{2}\right)^\dagger + \left(\frac{I-U}{2}\right)\ket{\psi}\bra{\psi}\left(\frac{I-U}{2}\right)^\dagger$$

That gave me the idea for the following circuit decomposition:

Summing up the density matrices of the 2 circuits results in the density matrix $\rho$.

However, the gate $(I\pm U)/2$ is not unitary. Is there a way to implement $(I\pm U)/2$ on a quantum computer?

Answer 1

You can use a linear combination of unitaries (LCU).

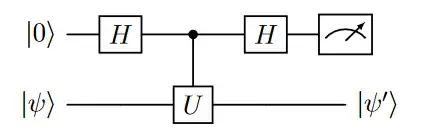
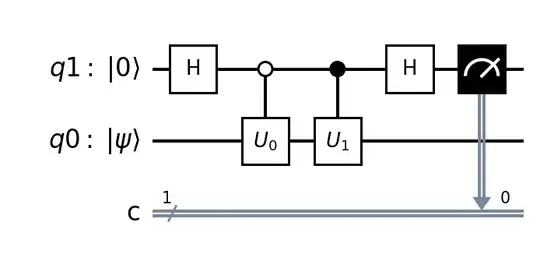
Consider the following circuit, where $q_1$ is initialized at $|0\rangle$ and $q_0$ has the state $|\psi\rangle$ you want to evolve:

After the first $H$ gate, you have the state:

$$\frac{1}{\sqrt{2}} \left(|0\rangle + |1\rangle \right) \otimes |\psi\rangle $$

As for the controlled gates, $U_0$ gets applied on $|\psi\rangle$ if $q_1$ is $|0\rangle$, and $U_1$ gets applied if $q_1$ is $|1\rangle$, so you end up with the state:

$$\frac{1}{\sqrt{2}} \left(|0\rangle \otimes U_0 |\psi\rangle + |1\rangle \otimes U_1 |\psi\rangle\right) $$

Then, after the second Hadamard gate you have:

$$ \frac{1}{\sqrt{2}} \left(\frac{1}{\sqrt{2}} \left(|0\rangle + |1\rangle \right) \otimes U_0 |\psi\rangle + \frac{1}{\sqrt{2}} \left(|0\rangle - |1\rangle \right) \otimes U_1 |\psi\rangle\right) .$$

Reorganizing by factorizing over $q_1$:

$$ \frac{1}{2} \left(|0\rangle \otimes (U_0 + U_1) |\psi\rangle + |1\rangle \otimes (U_0 - U_1) |\psi\rangle\right) . $$

So, if you perform a measurement on $q_1$ and post-select the state $|\psi\rangle$ for when you measure $|0\rangle$, you get the state:

$$\frac{1}{2} (U_0 + U_1) |\psi\rangle, $$

up to a normalization factor.

Similarly, if you post-select for a measurement of $|1\rangle$, you get the state:

$$\frac{1}{2} (U_0 - U_1) |\psi\rangle, $$

again, up to a normalization factor.

You can then replace $U_0$ with $I$ (although that will be equivalent to not applying that gate), and $U_1$ with $U$.

So basically you end up with the same circuit used for the Hadamard test, you're just post-selecting based on the measurement result. Just figured I would frame it in terms of an LCU since the concept can be applied more generally.