doesn't a reset on an entangled qubit collapse a superposition?

Question

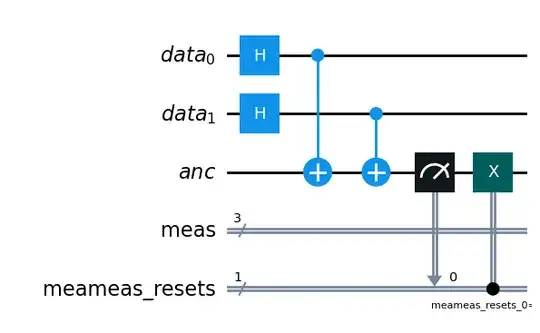
When I reset an entangled qubit then measure it looks a superposition isn't collapsed to a certain states.

In my experiment, the state just before applying a reset is: $$\frac{1}{2}(|000⟩+|011⟩+|101⟩+|110⟩)$$

then I reset an ancillary qubit(the right most qubit) to $0$. At this point, I think the state should be changed to: $$\frac{1}{\sqrt{2}}(|000⟩+|110⟩)$$ because superposition $|01⟩$ or $|10⟩$ cannot be taken as entangled qubit is already reset to $0$.(am I right?)

However, the measurement result shows the superposition isn't collapsed to $|00⟩$ or $|11⟩$, in fact it has all of the 4 states $|00⟩$,$|01⟩$,$|10⟩$ and $|11⟩$.

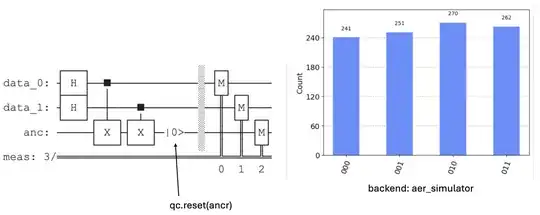
My question is, doesn't a reset on an entangled qubit make an entangled superposition collapse to a certain states? I'd appreciate any comment! (FYI, reproduction code is attached)

#qiskit 1.0.2
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile
from qiskit_aer import AerSimulator, Aer
from qiskit.visualization import plot_histogram, plot_bloch_multivector, plot_distribution, circuit_drawer
from qiskit.quantum_info import Statevector
from qiskit_ibm_runtime import QiskitRuntimeService
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
from qiskit_ibm_runtime import Session, SamplerV2 as Sampler
datar = QuantumRegister(2, "data")
ancr = QuantumRegister(1, "anc")
measr = ClassicalRegister(3, "meas")
qc = QuantumCircuit(datar, ancr, measr)
qc.h([datar[0], datar[1]])
qc.cx(datar[0], ancr)
qc.cx(datar[1], ancr)
#qc.measure(ancr, measr[2])
qc.reset(ancr)
qc.barrier()
qc.reset(ancr)
qc.measure([datar[0], datar[1], ancr[0]], list(measr))
#qc.measure(datar[0], measr[0])
#qc.measure(datar[1], measr[1])
qc.draw()
aer = AerSimulator()
pm = generate_preset_pass_manager(backend=aer, optimization_level=1)
shots = 1024
isa_qc = pm.run(qc)
with Session(backend=aer) as session:
    sampler = Sampler(session=session)
    result = sampler.run([isa_qc], shots=shots).result()
pub_result = result[0]
counts = pub_result.data.meas.get_counts()
plot_histogram(counts)

score 2 · Accepted Answer · answered May 16 '24 at 10:42

In IBM quantum devices, reset instruction is implemented as a mid-circuit measurement followed by a conditional Pauli-X (see here). That means, your circuit is equivalent to the below circuit:

This should explain to you the result you have.

Another issue in your logic is this statement:

then I reset an ancillary qubit (the right most qubit) to 0.

Qiskit uses little-endian ordering for both classical bits and qubits (see here). That means, the ancillary qubit is the left-most qubit.

doesn't a reset on an entangled qubit collapse a superposition?

1 Answers1