Removing ancilla qubit from circuit with Hadamard test controlled-Z gate

Question

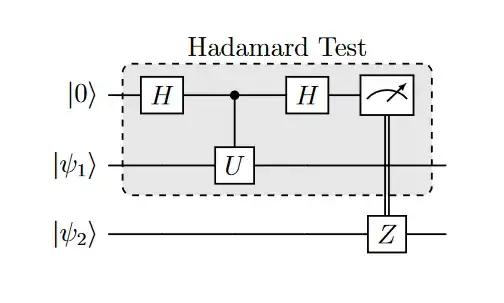
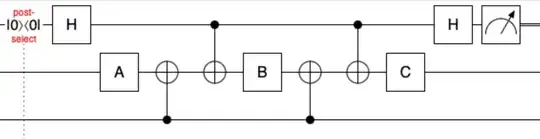
I want to remove the ancilla qubit from the following quantum circuit:

Is this possible?

The final state of $\newcommand{\ket}[1]{\vert#1\rangle}\newcommand{\bra}[1]{\langle#1\vert}\ket{\psi_1}$ is $\frac{1}{2}\left(\ket{\psi_1}\bra{\psi} + U\ket{\psi_1}\bra{\psi}U^\dagger\right)$. But I don't know how to create the final state of $\ket{\psi_2}$.

The paper Methodology for replacing indirect measurements with direct measurements presents a technique to measure the expectation value of a unitary $U$ without the Hadamard test. Would it be possible to somehow create the final state of $\ket{\psi_2}$ by measurements of $\ket{\psi_1}$ under some conditions?

Answer 1

For special unitaries $U$ you can use the standard decomposition of a controlled-$U$.

You can then try to move backward in the circuit the conditioned gate $Z$. According to the deferred measurement principle this is a controlled-$Z$ gate.

The result is something like this