Transversal CNOTs on CSS codes with multiple logical qubits

Question

I am interested in the theory of implementing logical gates on quantum error correcting codes. From a practical view, transversal gates are very attractive. I have a question about transversal gates.

Background

Here on stack exchange, I find many statements such as "Stabilizer code $\mathcal{G}$ is a CSS code if and only if $\mathcal{G}$ has transversal CNOT."(copied from a very nice answer to this question). These kind of statements are also to be found in other posts, for example here. Also, places like the error correction zoo page for CSS codes just write "All CSS codes admit transversal Pauli and CNOT gates" (In the section "Transversal gates").

What is in these two situation meant by transversal CNOT is - if I understand correctly - the following: If you have two copies $\mathcal{C}_1$, $\mathcal{C}_2$ of a $[[n,k,d]]$-CSS code $\mathcal{C}$ with physical qubits $q_1, \dots , q_n$ and apply CNOT between $q_1$ in the first code and $q_1$ in the second code and same for $q_2, \dots , q_n$, then

• this preserves the code space. This is because an $X$ type stabiliser $S_X \otimes id$ of $\mathcal{C}_1$ gets mapped to $S_X \otimes S_X$, that is, the same $X$-type stabiliser on both codes, and $id \otimes S_X$ get mapped to $id \otimes S_X$. So the $X$ type stabilisers for the two codes together are exactly preserved. Similar reasoning holds for the $Z$-type stabilisers.
• this, with the same reasoning as for the stabilisers, performs a logical CNOT between the logical qubits. Namely, if we say $\bar{X}_1, \dots , \bar{X}_k$ are independent choices logical $X$ operators that are products of $X$ and $id$ on the physical qubits, then applying all these CNOT gates on the physical qubits of the two codes will transform $\bar{X}_i \otimes \bar{id}$ to $\bar{X}_i \otimes \bar{X}_i$ for $i = 1 \dots k$ and similarly $\bar{id} \otimes \bar{X}_i$ gets transformed to $\bar{id} \otimes \bar{X}_i$. So what this operation did is, it applied all of the gates $CNOT_1, \dots , CNOT_k$ if my reasoning is correct.

My question

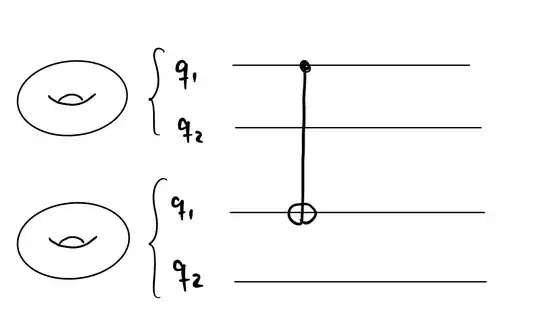
My question is the following: Can I do more "targeted" CNOT gates on CSS codes. For example, the toric code encodes two logical qubits $q_1$ and $q_2$. Can I transversally apply a CNOT between two copies of the toric code, but only the CNOT between one qubit in the first code and one in the second one? Here a very informal drawing:

One naïve idea would be to apply CNOT between qubits involved in the corresponding logical $X$ operator, but for the toric code, it doesn't seem to preserve the stabiliser group.

So very concretely, my questions are:

• Very practically and hands-on: Can I transversally apply the "single" CNOT on the toric code transversally? It would be totally fine if transversality here does not mean "a product of physical CNOTs between the two code patches" but the less restrictive "a product of physical one-qubit gates and physical two-qubit gates between the patches".
• More generally, for CSS code, is there any theory on which logical CNOTs one can actually do transversally? Is there more hiding behind the narrative that "CSS codes have transversal CNOT" than what I elaborated above? Is there a theory of which transversal CNOTs are possible on CSS codes? For example, for color codes, one often reads that 2D color codes can implement the Clifford group transversally. I completely see how that is true for color codes that encode only one qubit, but not for color codes with more than one logical qubit.

Answer 1

Expanding on DaftWullie's answer: it is sufficient to prepare "selection states".

Suppose you can prepare a "selection state" $|S_k\rangle$ where all the logical qubits are $|0\rangle$, except for the logical qubit with index $k$ which is in the state $|+\rangle$. You can use this state to mask out effects so they apply to that one qubit. And that kind of opens up the world.

For example, if you want to measure one qubit $k$, you can do that by consuming a copy of $|S_k\rangle$ using block-transversal CNOTs, Hs, and measurements (as well as non-block-transversal Pauli feedback in the control system). This is the selective measurement:

The key thing here is that the only gates controlled by the "selected" line are the CH at the start (representing preparation of the selection state) and the Pauli feedback at the end (which is easy to do non-transversally).

Selective measurement easily generalizes to selective parity measurement:

Once you have selective parity measurement, you can make the selective CNOT via lattice surgery. The selective CNOT gives you the selective swap. The selective swaps gives you everything, via selective temporarily-swap-to-an-ancillary-patch-and-do-the-gate-there.

So this has at least reduced the problem of doing selective gates to the problem of preparing these selection states. I suspect you can do that by preparing noisy versions, then doing some kind of state distillation, then using existing copies to catalyze the production of more copies.

Answer 2

As you say, when people talk about these transversal gates, they typically mean a physical transversal application, resulting in transversal logical application. Whether you can localise it to qubits depends on your code (and typically costs you one level of the Clifford hierarchy).

In particular, we always start with the ability to to individual Paulis in a transversal manner. Imagine we could do individual $S$ gates as well. This would give us the power to convert transversal $H$ into individual $H$ gates, using the identities $H^3=H$ and $(SH)^3=I$. (In other words, apply transversal $H$ 3 times. On qubits where you don't want to apply $H$, use your individual $S$ after each $H$.) I can also make individual c-Z because $X^2=I$ and $SXS^\dagger X=Z$, then replace $X$ with controlled-not.

If I don't have individual $S$, I can make it if I have transversal $T$, using $TXT^\dagger X=S$ and $TT^\dagger=I$, thereby converting the individual $X$ control into individual $S$.

There are other tricks that you can perform. For example, if you can prepare individual logical ancillas (in $|+\rangle$ states or $|0\rangle$) states (this is individual Pauli measurement, which isn't transversal), you can convert transversal $S$ + transversal cNOT into local $S$. This is basically gate teleportation.

For the Toric code, we don't have enough available to get started with any of these tricks.