13

Background:

In most setups of fault-tolerant quantum computation, universality is achieved using Clifford gates such as $(S, H, \text{CNOT})$ and the $T$-gate.

The Eastin-Knill theorem can be informally stated that it will be difficult (although possible through circumvention) to implement a universal set of gates fault-tolerantly.

Question:

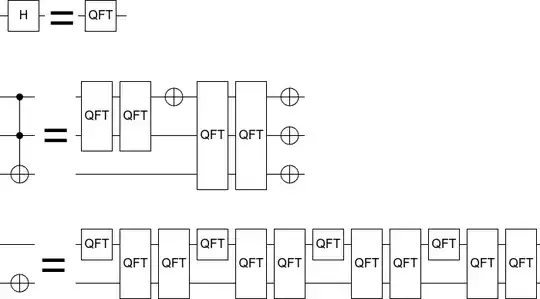
The Quantum Fourier Transform is an important primitive, but does there exist a finite gate set which is non-universal that generates the Quantum Fourier Transform?

FDGod
  • 2,901
  • 2
  • 6
  • 31
Frederik Ravn Klausen
  • 602
  • 4
  • 12

1 Answers1

18

Yes, the QFT requires universality. No, there isn't a non-universal gate set that implements the QFT. Just having the QFT as an operation is already computationally universal, because it can generate H+TOFFOLI:

enter image description here

Therefore anything that generates the QFT must also be computationally universal.

I bet you can prove the 2-qubit QFT is fully universal on its own, not just computationally universal, since it's non-Clifford and just randomly putting some together seems to generate weird looking angles.

Craig Gidney
  • 44,299
  • 1
  • 41
  • 116