Can you produce Non-Clifford gates via Lattice Surgery?

Question

Is there any theorem stating that lattice merge/split operations (or perhaps more generally, so-called gauge-fixing) cannot produce a non-Clifford gate that can complete the universal gateset for the surface code?

Answer 1

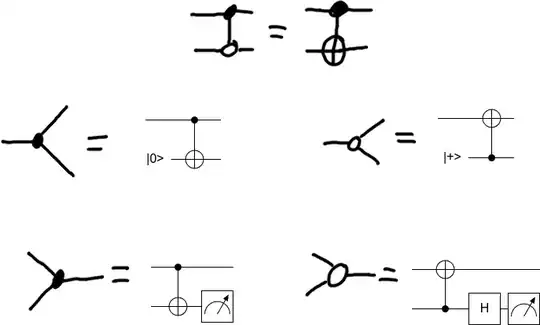
Merge and split can be performed with stabilizer operations (up to feedback due to ZX defining merge to use postselection whereas real computers have measurement instead):

Therefore if merge or split could do non-Clifford gates, you could do non-stabilizer gates with stabilizer gates.

You can't do non-Clifford (more generally: non-stabilizer) gates with only stabilizer gates and states. That's why they are called non-Clifford gates.

Therefore you can't do non-Clifford gates with merge and split operations.