Fault-tolerant correlated measurement on logical qubits

Question

So I have an encoded Bell pair $(|\overline{0}\overline{0}\rangle+|\overline{1}\overline{1}\rangle)$ in CSS code(e.g. Steane code) and I hope to perform stabilizer measurement of $\overline{XX}$ non-destructively. Can I simply perform Shor's style measurement on each side and combine their results? i.e. on each side, prepare ancillary $|0\rangle^{\otimes n}+|1\rangle^{\otimes n}$ and then do transversal CZ and measure in $\overline{X}$ basis? of course, I do this measurement 3 times to ensure fault-tolerance in the case of Steane code.\ I have doubt because this measurement is like, correlated, so maybe they should share an entangled ancillary state to begin with as well? Or is this independent measurement fine?

Answer 1

This approach will get you the correct measurement result, but will also collapse the encoded state.

Consider first the case with no underlying stabilizer code. You start with your Bell pair $\left|00\right\rangle + \left|11\right\rangle$ and measure $X_1$ and $X_2$ separately.

These measurement outcomes will be correlated, they will both give both +1 (or -1), which will collapse the state to $\left|+\right\rangle\otimes\left|+\right\rangle$ (or $\left|-\right\rangle\otimes\left|-\right\rangle$). However, you can reconstruct the measurement outcome of $X_1X_2$ by multiplying the two measurement outcomes of $X_1$ and $X_2$. This product gives +1 in all cases, which is not surprising since $X_1X_2$ was a stabilizer of your initial state.

In general, you can infer the measurement outcome of any Pauli operator that is a product of commuting measured Pauli operators.

Note that measuring $X_1$ and $X_2$ separately has a side effect: you initial state stabilized by $X_1X_2$ and $Z_1Z_2$ is now stabilized by $X_1X_2$ and $\pm X_1$ (and equivalently $\pm X_2$). This is probably not what you want, i.e. you should probably only measure $X_1X_2$ in one go.

The analysis is the same for the encoded case, your measurements are just more involved.

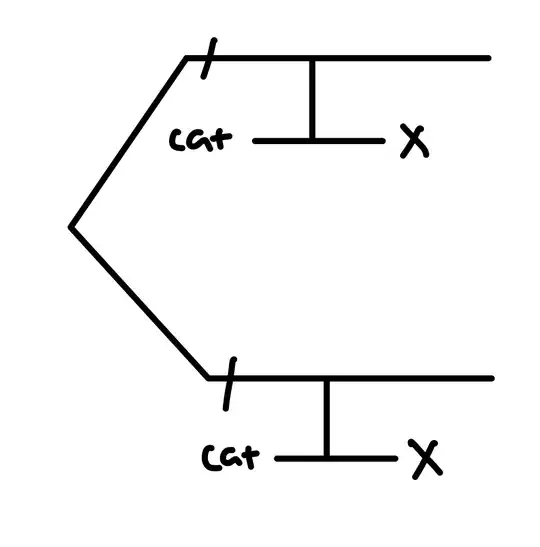
As mentionned in a comment, if you entangle your cat states in a big $\left|00\right\rangle^{\otimes n} + \left|11\right\rangle^{\otimes n}$, proceed with your Shor measurement and measure the $2n$ ancillary qubits at once, you should only be measuring your stabilizer operator.