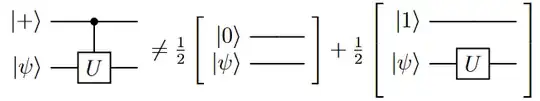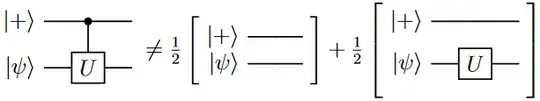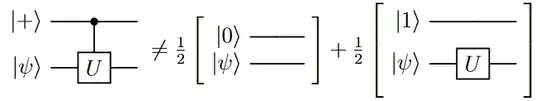$\newcommand{\ket}[1]{\vert#1\rangle}\newcommand{\bra}[1]{\langle#1\vert}$
Given a quantum circuit with 2 qubits that executes a controlled gate $CU$ where the control qubit is in the $\ket{+}$ state, and the target qubit is in an arbitrary state $\ket{\psi}$.
Intuitively, I would assume that this circuit can be decomposed into two circuits, one with initial state $\ket{0}\ket{\psi}$ that doesn't execute $U$ on the target qubit, and one with initial state $\ket{1}\otimes\ket{\psi}$ that executes $U$ on the target qubit. The idea is that the control qubit, when measured, will be 0 in 50% of the shots ($U$ is not executed) and 1 in the other 50% of the shots ($U$ is executed).
However, from doing the math, I came to the conclusion that this doesn't work:
Leaving the initial state as $\ket{+}\otimes\ket{\psi}$ does not work either:
I assume the phase kickback is the problem here.
Is there a way to to decompose the $CU$ gate into 1-qubit operations when the control qubit is in state $\ket{+}$?
My calculations:
Let $U=\left[\begin{matrix}u_{0} & u_{1}\\u_{2} & u_{3}\end{matrix}\right]$, $CU=\left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & u_{0} & u_{1}\\0 & 0 & u_{2} & u_{3}\end{matrix}\right]$, and $\ket{\psi} = \begin{bmatrix} a \\ b \end{bmatrix} \\\\$.
\begin{align*} CU(\ket{+}\otimes\ket{\psi})(\bra{+}\otimes\bra{\psi})CU^\dagger &= \frac{1}{2}\left[\begin{matrix}a \overline{a} & a \overline{b} & a \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & a \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\\b \overline{a} & b \overline{b} & b \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & b \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\\\left(a u_{0} + b u_{1}\right) \overline{a} & \left(a u_{0} + b u_{1}\right) \overline{b} & \left(a u_{0} + b u_{1}\right) \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & \left(a u_{0} + b u_{1}\right) \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\\\left(a u_{2} + b u_{3}\right) \overline{a} & \left(a u_{2} + b u_{3}\right) \overline{b} & \left(a u_{2} + b u_{3}\right) \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & \left(a u_{2} + b u_{3}\right) \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\end{matrix}\right] \\ & \neq \frac{1}{2}\left[\begin{matrix}a \overline{a} & a \overline{b} & 0 & 0\\b \overline{a} & b \overline{b} & 0 & 0\\0 & 0 & \left(a u_{0} + b u_{1}\right) \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & \left(a u_{0} + b u_{1}\right) \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\\0 & 0 & \left(a u_{2} + b u_{3}\right) \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & \left(a u_{2} + b u_{3}\right) \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\end{matrix}\right] \\ & = \frac{1}{2} \left( (\ket{0}\otimes\ket{\psi})(\bra{0}\otimes\bra{\psi}) + (\ket{1}\otimes U\ket{\psi})(\bra{1}\otimes U\bra{\psi}) \right) \end{align*}
\begin{align*} CU(\ket{+}\otimes\ket{\psi})(\bra{+}\otimes\bra{\psi})CU^\dagger &= \frac{1}{2}\left[\begin{matrix}a \overline{a} & a \overline{b} & a \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & a \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\\b \overline{a} & b \overline{b} & b \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & b \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\\\left(a u_{0} + b u_{1}\right) \overline{a} & \left(a u_{0} + b u_{1}\right) \overline{b} & \left(a u_{0} + b u_{1}\right) \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & \left(a u_{0} + b u_{1}\right) \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\\\left(a u_{2} + b u_{3}\right) \overline{a} & \left(a u_{2} + b u_{3}\right) \overline{b} & \left(a u_{2} + b u_{3}\right) \left(\overline{a} \overline{u_{0}} + \overline{b} \overline{u_{1}}\right) & \left(a u_{2} + b u_{3}\right) \left(\overline{a} \overline{u_{2}} + \overline{b} \overline{u_{3}}\right)\end{matrix}\right] \\ & \neq \frac{1}{4}\left[\begin{matrix}a \overline{a} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{0}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{1}} & a \overline{b} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{2}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{3}} & a \overline{a} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{0}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{1}} & a \overline{b} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{2}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{3}}\\b \overline{a} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{0}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{1}} & b \overline{b} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{2}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{3}} & b \overline{a} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{0}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{1}} & b \overline{b} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{2}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{3}}\\a \overline{a} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{0}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{1}} & a \overline{b} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{2}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{3}} & a \overline{a} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{0}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{1}} & a \overline{b} + \left(a u_{0} + b u_{1}\right) \overline{a} \overline{u_{2}} + \left(a u_{0} + b u_{1}\right) \overline{b} \overline{u_{3}}\\b \overline{a} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{0}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{1}} & b \overline{b} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{2}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{3}} & b \overline{a} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{0}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{1}} & b \overline{b} + \left(a u_{2} + b u_{3}\right) \overline{a} \overline{u_{2}} + \left(a u_{2} + b u_{3}\right) \overline{b} \overline{u_{3}}\end{matrix}\right] \\ & = \frac{1}{2} \left( (\ket{+}\otimes\ket{\psi})(\bra{+}\otimes\bra{\psi}) + (\ket{+}\otimes U\ket{\psi})(\bra{+}\otimes U\bra{\psi}) \right) \end{align*}