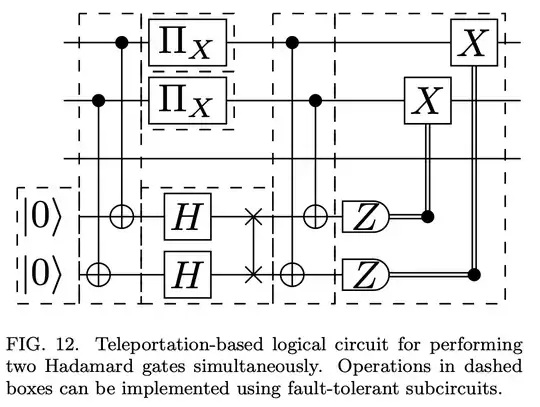
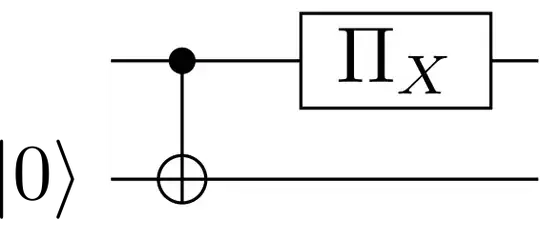
I'm trying to understand the circuit from Appendix A of the paper Fault-Tolerant One-Bit Addition with the Smallest Interesting Colour Code.
Here the top 3 qubits represent the 3 logical qubits of the $[[8,3,2]]$ color code (i'll call $|\psi\rangle$) and the bottom two are the two logical qubits of the $[[4,2,2]]$ code (I'll call $|\phi\rangle$). The problem being solved here is that there is no transversal Hadamard gate on the $[[8,3,2]]$, but there is on the $[[4,2,2]]$ code. So this circuit projects two qubits from $\psi$ onto $\phi$ using transversal CNOT, performs transversal Hadamard on $\phi$, and then teleports them back to $\psi$.
If anyone can provide a systematic explanation of how this circuit works, especially what the purpose of the logical $X$ measurements $\Pi_X$ and why the measurement controlled $X$ operators are done as they are that would be of great help.
The parts that are already clear to me are that performing Hadamard on the $[[4,2,2]]$ code is transversal (with a trivial swap) and there exist transversal CNOT gates between any two qubits of $\psi$ to $\phi$.
Recommendations for other sources to help understand these teleportation-type circuits would also be appreciated.
Thanks