How to inject a $\sqrt{X}$ gate, rather than Hadamard

Question

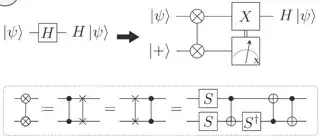
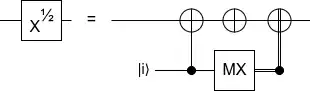
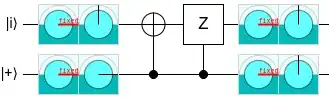
It follows the protocol for Hadamard gate injection:

Considering that $H \simeq \sqrt{Z}\sqrt{X}\sqrt{Z}$, it should be equivalent to inject $\sqrt{X}$ wrapped between $\sqrt{Z}$ gates.

I am led to think that $\sqrt{X}$ injection is possible, with some protocol that is somehow complementary to the $\sqrt{Z}$ injection.

However, I can't find it. Is it possible?

Answer 1

Notice that $\sqrt{X}=R_X(\pi/2)=HR_Z(\pi/2)H=H\sqrt{Z}H$. Therefore, you can principly perform the injection on the Z basis after a Hadamard gate on your state to be injected, and follow a Hadamard gate after you finish the injection.

Answer 2

Given the constraints, you can do it with phase kickback from a magic state:

Verification:

# note: uses "has_all_flows" which is currently only in stim 1.13.dev
import stim
assert stim.Circuit("""
    RY 1
    CX 1 0
    X 0
    MX 1
    CX rec[-1] 0
""").has_all_flows([
    stim.Flow("X0 -> X0"),
    stim.Flow("Y0 -> Z0"),
])

Note that you can replace $|i\rangle = |0\rangle + i|1\rangle$ with a $|+\rangle$ state followed by $\sqrt{Z}$, if needed. Also note that it's possible to duplicate $|i\rangle$ states by using RX,CX,CZ:

Also here's how you do a Hadamard with fewer gates:

assert stim.Circuit("""
    RX 1
    CX 1 0
    CZ 1 0
    MX 1
    Z 0
    CY rec[-1] 0
""").has_all_flows([
    stim.Flow("X0 -> Z0"),
    stim.Flow("Z0 -> X0"),
])