Measuring observables in the $[\![5,1,3]\!]$ code with stim

Question

Background

This question was triggered when I wanted to learn about stim and how to use it to run simulations for error correction. The resources I used for learning about stim were basically Craig Gidney's YouTube videos and his getting started-notebook.

Before I state my questions, I want to provide some background information (Everything I write is 'as I understand it' - if my thought process does not make sense anywhere, I'm more than happy for feedback!): The standard example to evaluate 'how good a code' is always goes like this example with the repetition code:

circuit = stim.Circuit.generated(
"repetition_code:memory",
rounds=2,
distance=3,
before_round_data_depolarization=0.04,
before_measure_flip_probability=0.01)

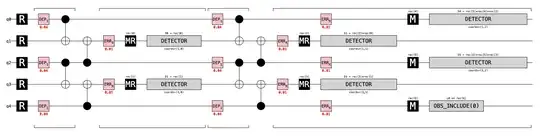
The circuit looks like this:

So, we are basically starting with the data qubits in state $|0\rangle^{\otimes 3}$, and then measure the observables (in this case $Z_1Z_2$ and $Z_2Z_3$) to get a logical $|0\rangle_L$ in repetition code (up to possible -1 outcomes which we don't care about). After performing as many error correction cycles as we feel like, we measure $Z_1$, $Z_2$, as well as $Z_3$, which each are logical $Z$ observables.

The neat thing now is that by measuring not only one logical observable (which in the noiseless case gives exactly as much information as measuring all three of them) but all three, we get once more syndrome information: We know that the product of the outcomes of the $Z_1$ and $Z_2$ measurements in the noiseless case would be equal to the outcome of the $Z_1 Z_2$ stabiliser measurement in the last error correction round. This is crucial: If, for example, in the whole circuit, there was no error happening, but in the very end, right before the logical measurement of the first qubit, there was an X-error, we would be screwed if we'd only measured this first qubit to measure the logical observable. But since we basically get one more round of repetition code error syndromes from these three observables $Z_1$, $Z_2$ and $Z_3$, our decoding algorithm can understand that the whole error syndrome flips the value of the logical observable $Z_1$.

---

My question

Now, I tried as an exercise to implement the $[\![5,1,3]\!]$ five-qubit perfect code.

It has stabiliser generators $XZZX\mathbb{1}$, $\mathbb{1}XZZX$, $X\mathbb{1}XZZ$ and $ZX\mathbb{1}XZ$.

It is, of course, not hard to implement (I guess non-fault tolerantly, but that is not the topic of this question...) the $[\![5,1,3]\!]$ code in stim:

perfect_code = stim.Circuit('''
H 0 1 2 3
DEPOLARIZE1(0.01) 0 1 2 3
CX 0 4
DEPOLARIZE2(0.01) 0 4
CZ 0 5
DEPOLARIZE2(0.01) 0 5
CZ 0 6
DEPOLARIZE2(0.01) 0 6
CX 0 7
DEPOLARIZE2(0.01) 0 7
CX 1 5
DEPOLARIZE2(0.01) 1 5
CZ 1 6
DEPOLARIZE2(0.01) 1 6
CZ 1 7
DEPOLARIZE2(0.01) 1 7
CX 1 8
DEPOLARIZE2(0.01) 1 8
CX 2 6
DEPOLARIZE2(0.01) 2 6
CZ 2 7
DEPOLARIZE2(0.01) 2 7
CZ 2 8
DEPOLARIZE2(0.01) 2 8
CX 2 4
DEPOLARIZE2(0.01) 2 4
CX 3 7
DEPOLARIZE2(0.01) 3 7
CZ 3 8
DEPOLARIZE2(0.01) 3 8
CZ 3 4
DEPOLARIZE2(0.01) 3 4
CX 3 5
DEPOLARIZE2(0.01) 3 5
H 0 1 2 3
DEPOLARIZE1(0.01) 0 1 2 3
M 0 1 2 3
R 0 1 2 3
H 0 1 2 3
DEPOLARIZE1(0.01) 0 1 2 3
CX 0 4
DEPOLARIZE2(0.01) 0 4
CZ 0 5
DEPOLARIZE2(0.01) 0 5
CZ 0 6
DEPOLARIZE2(0.01) 0 6
CX 0 7
DEPOLARIZE2(0.01) 0 7
CX 1 5
DEPOLARIZE2(0.01) 1 5
CZ 1 6
DEPOLARIZE2(0.01) 1 6
CZ 1 7
DEPOLARIZE2(0.01) 1 7
CX 1 8
DEPOLARIZE2(0.01) 1 8
CX 2 6
DEPOLARIZE2(0.01) 2 6
CZ 2 7
DEPOLARIZE2(0.01) 2 7
CZ 2 8
DEPOLARIZE2(0.01) 2 8
CX 2 4
DEPOLARIZE2(0.01) 2 4
CX 3 7
DEPOLARIZE2(0.01) 3 7
CZ 3 8
DEPOLARIZE2(0.01) 3 8
CZ 3 4
DEPOLARIZE2(0.01) 3 4
CX 3 5
DEPOLARIZE2(0.01) 3 5
H 0 1 2 3
DEPOLARIZE1(0.01) 0 1 2 3
M 0
DETECTOR rec[-1] rec[-5]
M 1
DETECTOR rec[-1] rec[-5]
M 2
DETECTOR rec[-1] rec[-5]
M 3
DETECTOR rec[-1] rec[-5]
M 4 5 6 7 8
OBSERVABLE_INCLUDE(0) rec[-1] rec[-2] rec[-3] rec[-4] rec[-5]

The following screenshot is probably a bit hard to decipher, but I guess if one is used to stim it might still help to see the coarse structure..

My problem/question is the following: I do not believe that we can apply a similar procedure as for the repetition code to protect ourselves from errors happening shortly before the final logical measurements. Here is a complete list of logical $Z$ operators on the [5,1,3] code (ignoring $\pm 1, \pm i$ prefactors).

$IIYZY$	$YIIYZ$	$XIZIX$	$ZIXXI$
$IXXIZ$	$YXZXY$	$XXIZI$	$ZXYYX$
$IYZYI$	$YYXZX$	$XYYXZ$	$ZYIIY$
$IZIXX$	$YZYII$	$XZXYY$	$ZZZZZ$

Looking at it, we can see that by picking $P_1, \dots , P_5$ single qubit Paulis that we measure on the data qubits, the best that we can achieve is that we get information about two different representatives of the logical operator and about one of the stabilisers, e.g.:

$$ P_1 = X\,,\\ P_2 = Z\,, \\P_3 = X\,,\\ P_4 = Z\,,\\ P_5 = Z\,,$$

gives information about the representatives $IZXZI, XZIIZ$ of $Z_L$ as well as the stabiliser $XIXZZ$. In this case, an X-error on the second system would screw everything up and would let us think the outcome is the opposite of what it was supposed to be (and it would be consistent with all other information we have!)

I also wrote some script that tries all possibilities of Paulis one can measure and this is indeed the best one can do I think.

I tried to find this 'phenomenon' in the literature but I never found it mentioned anywhere.

I would be super happy to get any feedback on this. A few precise questions I would be happy to get an answer for:

• I feel like there should be a theory about what I just described, like a theory of when it is possible to reliably measure logical operators (by measuring single Paulis) and when not. I would be very happy to get some references if this has been studied before.
• My intuition is that for CSS codes, the described problems cannot occur. (Proof sketch: For CSS codes, the stabilisers and the logical operators can be chosen as products of only $Z$s or of only $X$s. So, if we measure all data qubits in $Z$ basis, we get another round of $Z$ type syndromes for free as well as the value of logical $Z$ operator we are interested in. If a $Z$-type error would happen shortly before the final, logical measurement, this wouldn't affect the outcome of the single qubit $Z$ measurements. If an $X$-error happens, it would affect the outcomes but it can be detected from the additional stabiliser syndromes.)
• Are there non-CSS codes for which this problem can be avoided?

Answer 1

There are two problems you're running into: initialization and hook errors. These are common problems to run into when considering full circuit noise.

Hook Errors

Suppose an X error occurs on the measurement qubit halfway through performing the CX and CZ gates that you've decomposed a four-body measurement into. This error anticommutes with the following two controlled gates, causing it to spread to their targets, creating two data errors.

Hook errors are tricky because they're often worth multiple data errors. You have to be very careful about the order you do things, to avoid hook errors reducing the distance. In the case of the [[5,1,3]] code I doubt there's any ordering that works, because the set of possible symptoms is 1:1 with the set of single qubit errors so there's no room left to describe these 2 qubit errors.

One way to bypass the hook error problem is to change the strategy you are using for measuring the stabilizers. Well known strategies are "the steane method" and "the Shor method", as well as flag qubits which catch the hook error by using two measure qubits prepared in $|00\rangle + |11\rangle$ instead of one measure qubit prepared in $|+\rangle$.

Initialization / Measurement

It's a nice property of the repetition code that just preparing all the data qubits into the $|0\rangle$ state is a fault tolerant preparation of logical $|0\rangle$. This is a special property that not all codes have. This property is called transversal $R_Z$. The [[5,1,3]] code doesn't have it.

A well known family of codes with transversal $R_Z$ is CSS codes. They also have transversal $R_X$, $M_X$, and $M_Z$ (also $CX$). For example, the surface code is a CSS code and it correspondingly has transversal $M_X$, $M_Z$, $R_X$, and $R_Z$. The color code is also a CSS code, so it also has those transversal gates, but it actually goes even further and adds on transversal $R_Y$ and $M_Y$ (which not all CSS codes have).

Just because you can't do initialization transversally, that doesn't mean there's no way to do fault tolerant initialization. It just means the simplest possible thing didn't work.

• In the XZZX surface code, logical $R_Z$ and $R_X$ are implemented by preparing some data qubits into $|0\rangle$ and some into $|+\rangle$, with the pattern depending on the logical state you want. That's not literally broadcasting the desired operation over the data qubits, so it's not strictly speaking "transversal", but it's still very simple and cheap. It didn't even need any two qubit gates.
• In the folded surface code, a fault tolerant logical $R_Y$ can be done in constant depth by doing logical $R_X$, then doing one round of stabilizer measurement, then doing a logical $S$ gate (implemented with a layer of $S$ gates along the fold, and $CZ$ gates between qubits lined up with each other due to the fold). The round of stabilizer checks isn't strictly speaking necessary, but it avoids the code distance getting cut in half by the $CZ$ gates touching pairs of qubits.
• In the surface code, there is no constant depth fault tolerant $R_Y$ with no long range gates (as far as I know). But it has a no-long-range-gates fault-tolerant $R_Y$ based on braiding twists over d/2 rounds.
• Non-Clifford states like $T |+\rangle$ often require super elaborate preparations to make them fault tolerant (like magic state injection and distillation).

Offhand, I don't know a simple way to prepare the [[5,1,3]] code that has distance 3 fault tolerance. It's definitely possible. For example, you could concatenate over the surface code during the initialization, relying on the surface codes to prevent all errors during that time using the surface codes, then drop out of the surface codes into the normal [[5,1,3]] code. But probably there are papers out there describing much more compact procedures.