The above circuit shows a first measurement, which is $\langle X \rangle$ or $\langle Y \rangle$, depending on the outcome of a second measurement.
Assuming now that a third measurement decides whether applying a Pauli $X$ as in the above picture. Is it possible to make the $X$ operation classical? Meaning that it operates over the bit given by the upper measurement.
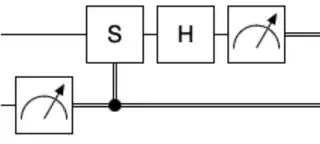
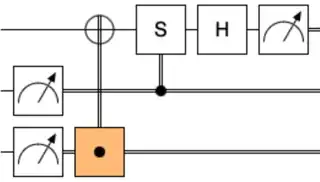
A trick you can use in this situation is "control splitting". Replace "do X" with "do X if C; also do X if not C". Do this:
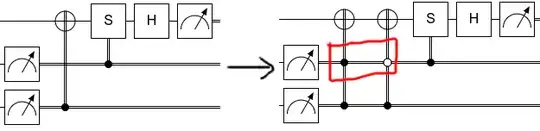
Now you can advance each case individually. The NOT whose control matches the S gate's control gets conjugated by the S into a Y, while the NOT whose control disagrees with the S gate's control just passes through. The H then then turns the Y into -Y and the X into Z. The - is irrelevant because the controls are classical, so we drop it:
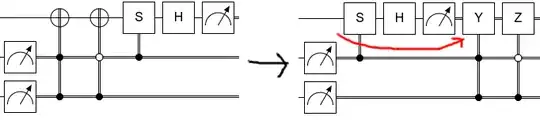
Phasing bits does nothing, so you can then just delete the Z gate and also simplify the Y into an X:
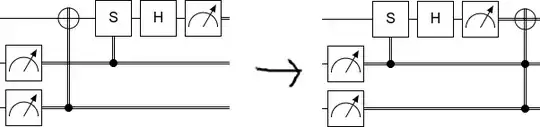
Looking back at a high level, you can see that this makes sense. The X matters when you're measuring $\langle Y \rangle$, but it doesn't matter when you're measuring $\langle X \rangle$, so you end up flipping the measurement only in the case where it mattered.
