I am trying to implement Shor's algorithm using modular exponentiation as described in this paper: https://arxiv.org/abs/quant-ph/0205095
The issue is found when trying to implement CMULT($a^{-1}$)mod(N)
Since we can only use integers, do you know how to inject $a^{-1}$ into the algorithm?
$a^{-1}$ is an integer, because you're working in modular arithmetic.
$a^{-1}$ is the value that satisfies $a \cdot a^{-1} = 1$. For example, on a clock, 5-oclock times 5-oclock equals 25-oclock which is the same as 1-oclock so a solution to $5x = 1 \pmod{12}$ is $x=5$ meaning $5^{-1} = 5 \pmod{12}$.
In python you can compute multiplicative inverses mod N by using pow:
N = 101*103
a = 52
a_inv = pow(a, -1, N)
print(a_inv) # 3401
print(a * a_inv) # 176852
print(a * a_inv % N) # 1
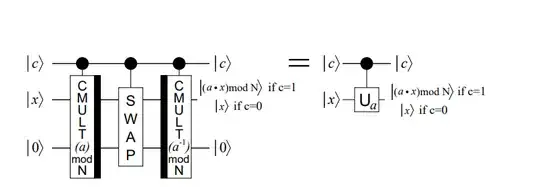
Given two coprime integers $a$ and $N$, you can compute $a^{-1} \text{ mod } N$ efficiently classically by using the extended Euclidean algorithm even if the factorization of $N$ is unknown. This is what saves you.
To see this easily, note that said algorithm gives you integers $u, v$ and $d$ such that $ua + vN = d = \gcd(a, N) = 1$. It follows that $ua \equiv 1 \:\: (\text{mod } N)$ and hence that $u \equiv a^{-1} \:\: (\text{mod } N)$.
(Note also that had we know the order $r$ of $a$ perceived as an element of a cyclic subgroup to $\mathbb Z_N^*$, then we could have used that $a^{-1} \equiv a^{r-1} \:\: (\text{mod } N)$ to find the inverse $a^{-1} \text{ mod } N$. This technique generalizes to any cyclic group, and so may be useful for taking inverses efficiently classically when implementing Shor's algorithm for computing discrete logarithms — if needed to implement the arithmetic, and if the group in question does not admit a more efficient algorithm for taking inverses. But in Shor's order-finding algorithm, the order $r$ of $a$ can of course not be assumed to be classically known.)
