PyMatching finds the minimum weight matching, which will belong to a particular equivalence class. But sometimes it is useful to know the minimum matching of each equivalence class.
In the olden days, when we build our own matching decoders with lots of virtual nodes, this could be done by suitably tweaking the graph. I'm not sure how those methods can be ported over to PyMatching though.
Is there an easy trick I'm missing?
As you noted in your self-answer, you can force pymatching to attach to a boundary an even or odd number of times by turning the boundary into a detector node and forcing its value to be 0 (attach even number of times) or 1 (attach odd number of times). You can then compare the weight of the two matchings (pass return_weight=True into decode_batch): the lower-weight result is the normal matching, and the higher-weight result is the complementary matching.
For example, this is how we computed the complementary matchings in "Yoked Surface Codes". You can see me inverting the extra detector in the source code here. We also did some statistics on the gaps, showing they're well behaved:
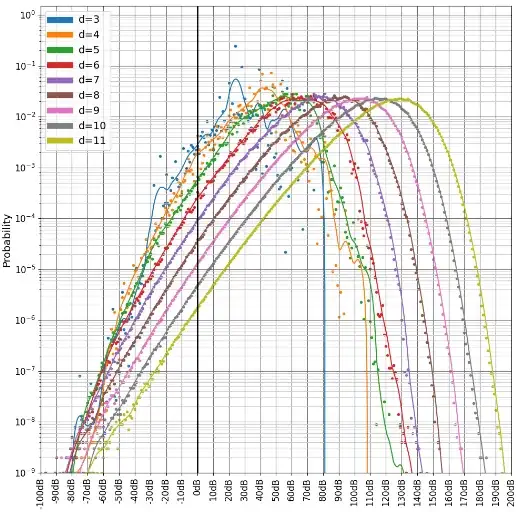
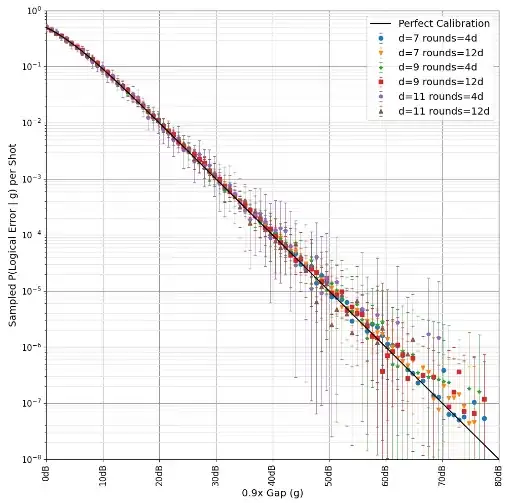
There are a few problems with this approach to computing the gap, when you start trying to do this for circuits more complicated than memory experiments (e.g. magic state distillation):
You need to identify all the topologically distinct boundaries. This is tedious. Go on, count them:
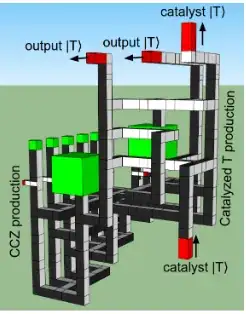
Cost scales exponentially in the number of distinct boundaries (or in the number of logical qubits). You're trying all the variations to find the smallest variation.
It assumes the difference between the matchings will involve a boundary in the first place! In a toric code, the complementary matching differs from the normal matching by a cycle instead of by a path. Potential cycle differences are also created when doing lattice surgery more complicated than a single parity measurement.
It puts pymatching into a worst case peformance scenario. Pymatching's speed comes from knowing that the matching will end up being a lot of small clusters. The complementary matching exactly violates that, forcing a blossom to grow all the way from one side of the patch to the other. This can easily be thousands of times slower.
This technique is incompatible with faster union-find decoders. The cluster growing from the boundary you turned into a detector node can't terminate until it reaches the other boundary. So it tends to just fuse all the detection events into one big cluster.
I think the way to avoid most of these costs is to (1) focus on just computing the numerical value of the complementary gap (instead of returning the exact matchings and having the user compute their difference from that) and to (2) turn it from a matching problem into a minimum path length problem.
I'm reasonably sure these can be achieved by taking pymatching's full state as it finishes decoding, zeroing the weight of all edges that are in a graph fill region (or partially reducing, when the edge is partially crossed), and then performing a Djistra search from one boundary to the other. I talked to someone at QEC who also had this idea and actually implemented it; hopefully they'll put out the paper soon. This zeroing-then-pathing approach also works for union-find decoders, since they also have reasonably-well-behaved graph fill regions.
One thing you could do to avoid brute force exploration of all logical qubit assignments in a magic state factory is to focus on one observable at a time. For each observable, make two copies of the graph: one is the starting copy and the other is the "crossed the observable while getting here" copy. The two copies are then spliced together at edges crossing the observable. The shortest path search can then done by starting from the boundaries of the normal graph, and searching for any boundaries in the "crossed the observable while getting here" graph using Dijkstra's algorithm. This should scale linearly with the number of observables, and avoids ever putting pymatching in its worst case scenario. Also it gives you a separate gap for each observable, which can be useful.
Unfortunately, I don't know a sufficiently efficient way to look for shortest cycles instead of shortest paths.
After asking the question, I think I figured out the answer.
For the example of the surface code, you need to have two boundary nodes rather than just one. One of these is connected to all the nodes on one side of the graph, and the other to the nodes on the other side. Let's call these the left and right boundaries.
Now say that, for some syndrome, the matching connects an odd number of times to the left boundary. The opposite equivalence class then corresponds to matchings that connect an even number of times to the left boundary.
To achieve this, create a new graph for which the left boundary node actually has is_boundary=False. Whether it is matched or not is then controlled by its value in the syndrome. So by assigning it a syndrome value of 0, the matching is forced into the opposite equivalence class.