Algorithmic Benchmark: What is the reason for unevenness (spike) in the runtime graph by the number of qubits of the Deutsch-Jozsa algorithm?

Question

I am testing quantum simulators based on runtime and memory usage. I impelmented Deutsch-Jozsa algorithm as follows in Qiskit:

def main():
    """
    Executes the Deutsch-Jozsa algorithm using the specified
    number of qubits and shots.
    """
    oracle = deutsch_jozsa_oracle(args.num_qubits)
    circuit = deutsch_jozsa_algorithm(oracle)
    backend = get_backend(args.provider, args.backend)
    transpiled_circuit = transpile(circuit, backend)
    backend.run(transpiled_circuit, shots=args.num_shots).result()
def deutsch_jozsa_oracle(num_qubits: int) -> QuantumCircuit:
    """
    Creates a quantum circuit representing the oracle for the Deutsch-Jozsa
    algorithm.
Args:
    num_qubits (int): The number of qubits in the circuit.

Returns:
    QuantumCircuit: The quantum circuit representing the oracle.
"""
oracle = QuantumCircuit(num_qubits + 1)

if randint(0, 1):
    oracle.x(num_qubits)

if randint(0, 1):
    return oracle

on_states = sample(range(2**num_qubits), 2**num_qubits // 2)

def add_cx(circuit, bit_string):
    for qubit, bit in enumerate(reversed(bit_string)):
        if bit == "1":
            circuit.x(qubit)
    return circuit

for state in on_states:
    oracle = add_cx(oracle, f"{state:0b}")
    oracle.mcx(list(range(num_qubits)), num_qubits)
    oracle = add_cx(oracle, f"{state:0b}")

return oracle



def deutsch_jozsa_algorithm(oracle: QuantumCircuit) -> QuantumCircuit:
    """
    Implements the Deutsch-Jozsa algorithm.
Args:
    oracle (QuantumCircuit): The oracle circuit representing the function
    to be evaluated.

Returns:
    QuantumCircuit: The circuit implementing the Deutsch-Jozsa algorithm.
"""
num_qubits = oracle.num_qubits - 1
algorithm = QuantumCircuit(num_qubits + 1, num_qubits)
algorithm.x(num_qubits)
algorithm.h(range(num_qubits + 1))
algorithm.compose(oracle, inplace=True)
algorithm.h(range(num_qubits))
algorithm.measure(range(num_qubits), range(num_qubits))
return algorithm

and as follows in Cirq:

def main():
    """
    Executes the Deutsch-Jozsa algorithm using the specified
    number of qubits and shots.
    """
    qubits = LineQubit.range(args.num_qubits + 1)
    oracle = deutsch_jozsa_oracle(qubits)
    circuit = deutsch_jozsa_algorithm(qubits, oracle)
    backend = get_backend(args.provider, args.backend)
    backend.run(
        circuit, repetitions=args.num_shots
    )
def deutsch_jozsa_oracle(qubits: list[LineQubit]):
    """
    Constructs the oracle circuit for the Deutsch-Jozsa algorithm.
Args:
    qubits (list[LineQubit]): The list of qubits to be used in the circuit.

Returns:
    Circuit: The constructed oracle circuit.
"""
num_qubits = len(qubits) - 1
oracle = Circuit()

if randint(0, 1):
    oracle.append(X(qubits[-2]))

if randint(0, 1):
    return oracle

on_states = sample(range(2 ** (num_qubits)), 2 ** (num_qubits) // 2)

def add_cx(qubits, bit_string):
    circuit = Circuit()
    for qubit, bit in zip(qubits[:-1], bit_string):
        if bit == "1":
            circuit.append(X(qubit))
    return circuit

mct = ControlledGate(sub_gate=X, num_controls=num_qubits)

for state in on_states:
    oracle.append(add_cx(qubits, f"{state:0b}"))
    oracle.append(mct(*qubits))
    oracle.append(add_cx(qubits, f"{state:0b}"))

return oracle



def deutsch_jozsa_algorithm(qubits: list[LineQubit], oracle: Circuit) -> Circuit:
    """
    Implements the Deutsch-Jozsa algorithm.
Args:
    qubits (list[LineQubit]): The list of qubits to be used in the algorithm.
    oracle (Circuit): The oracle circuit representing the function to be evaluated.

Returns:
    Circuit: The circuit implementing the Deutsch-Jozsa algorithm.
"""
algorithm = Circuit()
algorithm.append([X(qubits[-1]), H.on_each(*qubits)])
algorithm.append(oracle)
algorithm.append([H.on_each(qubits[:-1]), measure(qubits[:-1], key="result")])
return algorithm

I have tried to make the implementations so that a fair comparison can be made. All the executions were done on a personal computer with 16GB RAM and normal CPU. The expected output was that as the number of qubits increased, the execution time increased linearly or exponentially, but the graph I obtained after averaging 5 different executions for each simulator, shows a strange behavior! Here it is:

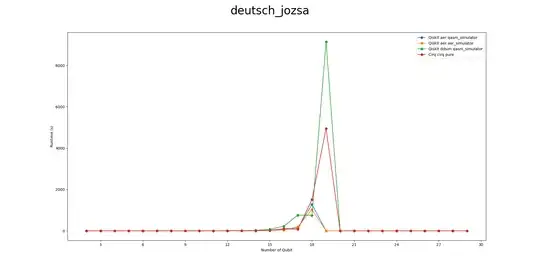
What is the problem?! Is there an implementation error on my part?!

Thanks in advance for your responses.