Is it possible to decompose an $n$-controlled Toffoli into $O(n)$ CNOTs without extra working qubits?
If so, is such an decomposition currently available in Qiskit or any other (preferably Python and QASM-friendly) packages?
If not:
Has such an impossibility been proven?
Is any decomposition into $O(n)$ CNOTs available in Qiskit or any other (preferably Python and QASM-friendly) packages?
In 2022, neither 2 nor 4 haven't apparently been implemented yet in Qiskit, see "Implemented by Qiskit:" here.
UPDATE
Using the following tket code (suggested in the answer below)
import qiskit
from pytket.extensions.qiskit import qiskit_to_tk, tk_to_qiskit
import matplotlib.pyplot as plt
import numpy as np
import pytket.transform as tkt
N = 10
qcs = []
cnots = []
x = np.array( range(1,145,9) )
for i,n in enumerate(x):
qc = qiskit.QuantumCircuit(n+1)
qc.mcx( list( range( n ) ), n )
# print(qc)
c = qiskit_to_tk( qc )
tkt.Transform.CnXPairwiseDecomposition().apply( c )
qc = tk_to_qiskit( c )
# print(qc)
if 'cx' not in qc.count_ops(): # At one value of n, instead of CX, controlled RX are produced
qc = qiskit.transpile( qc, basis_gates = [ 'u1', 'u2', 'u3', 'cx' ] )
cnot = qc.count_ops()[ 'cx' ]
print( f'Step {i+1}/{len( x )}; {n} qubits; {cnot} CNOTs' )
qcs.append( qc )
cnots.append( cnot )
fig, axs = plt.subplots( 1, 2 )
fig.suptitle( 'CNOTs' )
fig.set_size_inches( 10, 5 )
axs[ 0 ].plot( x, cnots, label = 'CNOTs')
axs[ 0 ].plot( x, x, label = 'x' )
axs[ 0 ].plot( x, 4xx, label = '4x^2' )
axs[ 0 ].plot( x, 200x, label = '200x' )
axs[ 0 ].set_xlabel( 'n of control qubits' )
axs[ 0 ].set_ylabel( 'CNOTs' )
axs[ 0 ].legend()
axs[ 1 ].loglog( x, cnots, label = 'CNOTs' )
axs[ 1 ].loglog( x, x, label = 'x' )
axs[ 1 ].loglog( x, 4xx, label = '4x^2' )
axs[ 1 ].loglog( x, 200x, label = '200x' )
axs[ 1 ].set_xlabel( 'n of control qubits' )
axs[ 1 ].set_ylabel( 'CNOTs' )
axs[ 1 ].legend()
plt.show()
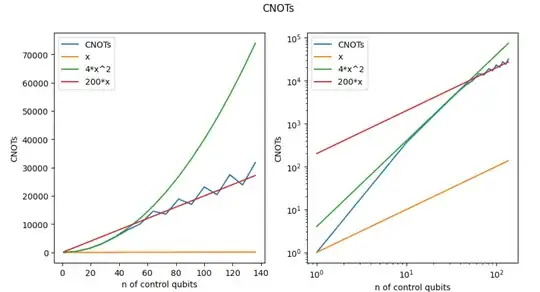
gives
The cost is quadratic up to 50 (!!) control qubits and then seems to be linear. This happens because under 50 qubits the tket function multi_controlled_to_2q() calls function CnU_linear_depth_decomp() for simplifying multi-controlled gates, and above 50 it switches to using CnX_normal_decomp(). (They claim that this is the right way to do things — and the plot kinda suggests that this is indeed the case.)
What surprises/upsets me is the factor of 200 in the linear regime — Craig Gidney's post provides a solution with ~16n Toffolis, each of which can be represented by 6 CNOTs.
UPDATE 2
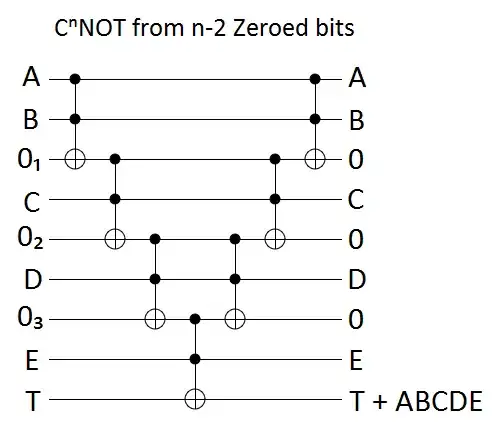
The implementation with $(n-2)$ (usual) ancillary qubits, as explained by Craig Gidney, requires $6(2n-3)=12n-18$ CNOTs, since each $n$-controlled gate is expanded into $(2n-3)$ Toffolis, each of which is decomposed into $6$ CNOTs:
from qiskit import QuantumCircuit, QuantumRegister, transpile
def mcx_decomposed( qr_c: QuantumRegister,
qr_t: QuantumRegister,
qr_anc: QuantumRegister ) -> QuantumCircuit:
"""
Decomposes the multi-controlled X gate into elementary gates.
:param qr_c: Control registers
:param qr_t: Target register
:param qr_anc: Ancilla registers
:return: Output circuit
"""
n = len( qr_c )
assert n >= 1, "The control register must contain at least one qubit."
assert len( qr_t ) == 1, "The target register must contain a single qubit."
assert n < 3 or len( qr_anc ) == n - 2, "The ancilla register must contain n - 2 qubits."
qc = QuantumCircuit( qr_c, qr_t, qr_anc )
if n == 1:
qc.cx( qr_c[ 0 ], qr_t[ 0 ] )
elif n == 2:
qc.ccx( qr_c[ 0 ], qr_c[ 1 ], qr_t[ 0 ] )
qc = transpile( qc, basis_gates = [ 'u1', 'u2', 'u3', 'cx' ] )
else:
qc.ccx( qr_c[ 0 ], qr_c[ 1 ], qr_anc[ 0 ] )
for i in range( n - 3 ):
qc.ccx( qr_anc[ i ], qr_c[ i + 2 ], qr_anc[ i + 1 ] )
qc.ccx( qr_anc[ n - 3 ], qr_c[ n - 1 ], qr_t[ 0 ] )
for i in range( n - 4, -1, -1 ):
qc.ccx( qr_anc[ i ], qr_c[ i + 2 ], qr_anc[ i + 1 ] )
qc.ccx( qr_c[ 0 ], qr_c[ 1 ], qr_anc[ 0 ] )
qc = transpile( qc, basis_gates = [ 'u1', 'u2', 'u3', 'cx' ], optimization_level = 3 )
return qc
To sum up:
- Without ancillas: $\approx 4n^2$ CNOTs for $n<50$, then $\approx 200n$ CNOTs.
- With $n-2$ ancillas: $12n-18$ CNOTs.