Let's assume I want to implement a rotation $R_Z(\theta)$ for a lattice-surgery based computation, for $\theta$ being an arbitrary angle (i.e. the gate is not necessarily Clifford nor a $T$-gate).
It can typically be done by
- Decomposing $R_Z(\theta)$ on Clifford+T gateset (possible up to some approximation $\epsilon$). I call $N_T$ the number of $T$-gates in the decomposition.
- The Clifford are "commuted" toward the end of the algorithm (we do the measurement based lattice surgery framework), which changes each of the $T$-gate in $\exp(-i P \pi/8)$ for some single-qubit Pauli $P$ (not anymore necessarily $Z$).
Hence, the duration of one $R_Z(\theta)$ should from my understanding be equal to $N_T$ logical timesteps. If we have many $R_Z(\theta)$ gates, the total duration of these gates should be $N_T \times D_R$ where $D_R$ is the depth associated to these gates (the number of layers containing at least one gate $R_Z(\theta)$).
However, while reading this paper (which explains the assumptions behind the Azure resource estimator), assuming no $T$-gates nor Toffoli nor measurements are in the end-user algorithm, they would find a total number of logical timestep, based on Eq (D3) on page 30:
$$C_{\min}=M_R+N_T \times D_R$$
What I call $N_T$ correspond to their $A \log_2(M_R/\epsilon)+B$ in their notation.
Basically, they add on my counting $M_R$ which is the total number of $R_Z(\theta)$ gates. Why should it be added? Isn't the term $N_T \times D_R$ sufficient?
[Edit]: Below is a concrete example showing why for me $C_{\min}=N_T \times D_R$ should be the formula (without $M_R$):
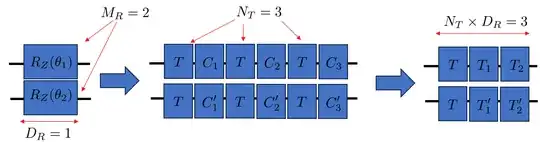
Left: two logical qubits are shown, on each of them I implement a $R_Z$ (of an angle that is not Clifford, and neither the one of a $T$-gate (i.e. not $\pi/4$).
Middle: this rotation is decomposed on Clifford+T gateset (the gates with label "C" represent single qubit Clifford).
Right: The Clifford are commuted through the $T$-gates. It results a circuit with only "generalized" $T$-gates (i.e. the rotation angle are $\pi/4$ but not necessarily around the $Z$ axis for the $T_i$).
In this example the circuit depth would be $N_T \times D_R$: I don't get why we should add $M_R$ on top.
The ancilla doing state injection are not represented in this image, but they would not change the number of logical timesteps (as doing one of the $T$-gate is essentially measuring a multi-Pauli observable which is done in a single timestep).