Once I get to the end of the algorithm, I can't understand how to calculate the eigenvalue using formulas. Bear in mind that it is an exercise to be carried out with pen and paper.
the matrix of $U$ is the following. $$ U = \begin{pmatrix} 0 & i \\ i & 0 \end{pmatrix}\,. $$
TL;DR: Qubit order in the top register is reversed.
Quirk's QFT gate treats the top qubit as the least significant and the bottom qubit as the most significant. Thus, if you feed the three-qubit QFT the computational basis state where the top qubit is $|1\rangle$ and all others are $|0\rangle$, then neglecting normalization the output will have amplitudes $$1, \omega_8, \omega_8^2, \dots, \omega_8^7\tag1$$ where $\omega_8=e^{\pi i/4}$. On the other hand, if you feed it the state with $|1\rangle$ in the bottom qubit and $|0\rangle$ elsewhere, then the output will have amplitudes $$+1,-1,+1,\dots,-1\tag2$$ again neglecting normalization.
Therefore, the first control should actually be on the top qubit and the last four controls should be on the bottom one.
Now, a three-qubit register can store the phase angles of the eigenvalues of $U$ as a fraction of $2\pi$ without any numerical error, so if the second register were set to an eigenvector of $U$ then the top register would end up in a computational basis state.
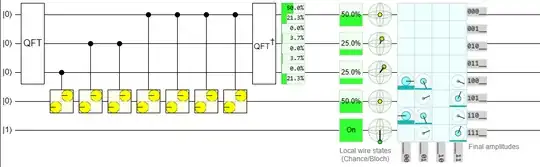
However, the second register does not store an eigenstate of $U$. It stores a superposition of two eigenstates. Therefore, once you have made the change I suggested above, you should be able to read off the phase angles corresponding to the two eigenvalues directly from the chance display: they should both have 50% chance of being read out.
You say that $U=iX$, but the picture suggests $U=-X$. If the former is correct, then the two non-zero values in the top register will be $.010$ (corresponding to eigenvalue $+i$) and $.110$ (corresponding to eigenvalue $-i$). If the latter is correct, then the two values will be $.000$ (corresponding to eigenvalue $+1$) and $.100$ (corresponding to eigenvalue $-1$).
