How to convert a partially entangled state into maximally entangled using SLOCC

Question

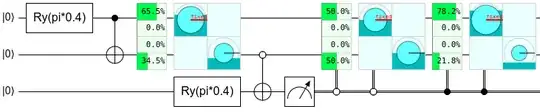
Let's say I have a generic partially entangled two-qubit state with Schmidt decomposition $$|\psi\rangle_{AB} = \sqrt{\alpha} |00\rangle_{AB} + \sqrt{\beta}|11\rangle_{AB}.$$

I know from Lo and Popescu (1999) and Vidal (1999) that the optimal probability of converting this state into the singlet $|\phi^+\rangle_{AB} = \frac{1}{\sqrt{2}} |00\rangle_{AB} + \frac{1}{\sqrt{2}}|11\rangle_{AB}$ using SLOCC is equal to $p_{\,\text{MAX}} = 2\beta$.

However, I'm unable to find any example of how this can be done (I also checked this related question here). I would love a simple example that perform this probabilistic operation, just to see how this can be done, even with non-optimal probability.

Answer 1

This case is pretty straightforward, if you're already familiar with generalised measurements. Assume $\alpha>\beta$ are real numbers. We can define $$ M_1=\left(\begin{array}{cc} \sqrt{\frac{\beta}{\alpha}} & 0 \\ 0 & 1 \end{array}\right). $$ Note that this is defined such that $(M_1\otimes I)|\psi\rangle\propto |\phi^+\rangle$. We then have to pick a multiplying factor to be as large as possible such that we can make $M_1$ part of a valid measurement. In particular, there needs to be a second measurement operator $M_2$ such that $$ M_1^\dagger M_1+M_2^\dagger M_2=I $$ and $M_2^\dagger M_2$ must be positive semi-definite. In the present case, we can have $$ M_2=\left(\begin{array}{cc} \sqrt{1-\frac{\beta}{\alpha}} & 0 \\ 0 & 0 \end{array}\right). $$

Now, if you work it out more carefully, $(M_1\otimes I)|\psi\rangle=\sqrt{2\beta}|\phi^+\rangle$. So, if you perform this measurement and get the 1 result (which happened with probability $2\beta$), the final state is $|\phi^+\rangle$. However, if you get the result 2, your output will be $|00\rangle$, and completely useless to you (from an entanglement perspective).

Answer 2

Here's a simple circuit construction. Not sure if it's optimal.

By using a CNOT gate onto a partially-rotated ancilla qubit, you get partial information about $|00\rangle$ vs $|11\rangle$. You can tune the rotation so that one of the measurement results gives a post-measurement state that's exactly $|00\rangle + |11\rangle$. The other measurement result is some other $\alpha_2 |00\rangle + \beta_2 |11\rangle$, with a worse balance than before, that you can repeat the technique on.

One round:

Three rounds

There's probably some simple way to get it done in a single round instead of in multiple rounds like this. It seems like using a second masking ancilla might do the trick, but I didn't see the easy way to compute the angles. You can see in the screenshot I'm close but not bang on (50.2:49.8 instead of 50:50).