Hadamard Gate on Cluster States

Question

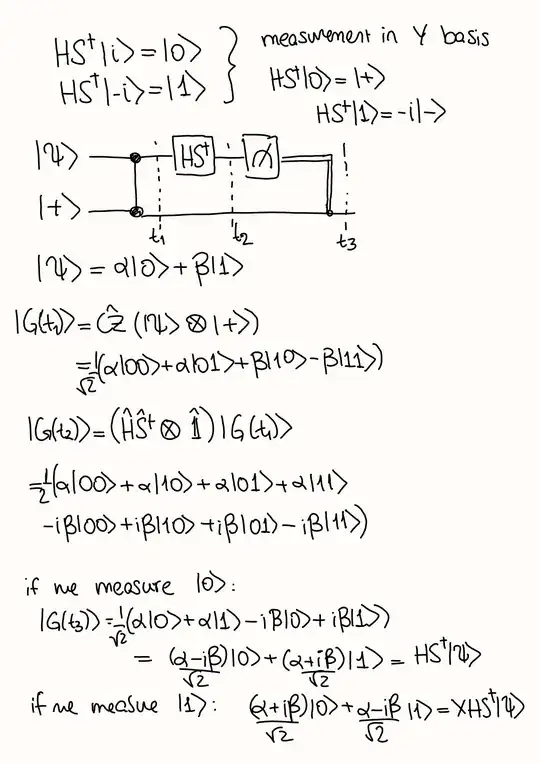
In measurement based quantum computing, according to R. Raussendorf, Hadamard Gate can be realized by five qubit cluster state, where the first qubit is measured in X basis and the following three are measured in Y basis.

However, even though I tried to calculate the outcome of the following measurements, I did not find Hadamard gate acting on initial state.

I assumed, to measure the qubit in X basis, we need to apply H gate and measure in Z basis:

\begin{equation} \mathbf{H} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \end{equation}

for measurements in Y basis, we apply a U gate and measure in the z basis, the required U gate is as follows:

\begin{equation} \mathbf{U} =\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & -i\\ 1 & i \end{bmatrix} \end{equation}

Now, measuring the state in those basis simply means applying those gates consecutively, except for additional X gates due to measurements, which we are not dealing right now. So, the result of this operation:

\begin{equation} \mathbf{X^{m_4}U X^{m_3}U X^{m_2}U X^{m_1}H}|\psi\rangle \end{equation}

which is not equal to:

\begin{equation} \mathbf{H}|\psi\rangle \end{equation}

However, if we only had 2 qubit cluster state and measure the first qubit in X basis, we would get:

\begin{equation} \mathbf{X^{m}H}|\psi\rangle \end{equation}

which is exactly Hadamard gate applied on initial state up to correction.

What am I missing here? Why don't we use two qubit cluster state in representation of Hadamard gate? How does this five qubit cluster state represents Hadamard gate?

Answer 1

Your calculation shows that you are doing the right thing for a single step. You just don't seem to be carrying it through for a set of 4 steps. Overall, you should be getting $$ (X^{m_4}HS)(X^{m_3}HS)(X^{m_2}HS)(X^{m_1}H)|\psi\rangle $$

For simplicity, assume that all the $m_i=0$, so you have the sequence $$ HSHSHSH. $$ Now there's a neat identity: $HSHSHS=I$ (up to a global phase), so you're left with just $H$.

Now, it's a fair question which you're faffing about with this sequence rather than just using a single step. Yes, you can get Hadamard from a single step, but the sequence of 4 things is a building block. By changing some of the measurement bases, you can get an arbitrary single-qubit rotation. But the Hadamard is the natural starting point for building up to that.