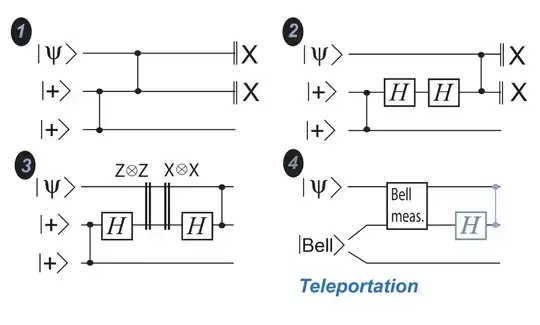
In step 2, you are doing two measurements, $X$ on qubit 1 and $X$ on qubit 2. To move to step 3, you need to bring these measurements earlier in the circuit, which means updating what they look like as they propagate through the other circuit elements.
Thankfully, controlled-phase is symmetric, so that reduces the amount of work we have to do. You just need to check the identity
$$
CP.(X\otimes I)=(X\otimes Z).CP
$$
This shows that the two $X$ measurements become measurements in $X\otimes Z$ and $Z\otimes X$ just before the controlled-phase. Then you also have to pull them through the Hadamard, which just converts $X$ and $Z$ and vice versa. Thus, your two measurements become $X\otimes X$ and $Z\otimes Z$. Note that since they commute with each other, it doesn't matter which of the two you write down first.
It is also unclear to me what it means to measure those qubits and
then continue with gates. Does it mean - take the post measurement
state and then apply those gates?
Yes, although the whole point of going from step 3 to 4 is to say "actually, we don't care about the post-measurement state". So if you're happy with that already, just make it part of the process in moving the measurements.