How is this step performed in Deutsch's algorithm?

Question

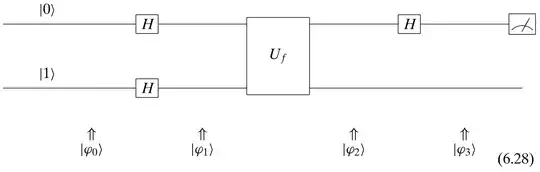
I am reading Quantum Computing for Computer Scientists. Given the circuit for Deutsch's algorithm:

Denoting $H|0\rangle$ as $|x\rangle$, the book says that

$|\phi_2\rangle = (-1)^{f(x)}|x\rangle\left\lbrack \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right\rbrack$

and then goes on to explain that because $|x\rangle$ is the superposed state $H|0\rangle$, this is the same as

$|\phi_2\rangle = \left\lbrack\frac{(-1)^{f(0)}|0\rangle + (-1)^{f(1)}|1\rangle}{\sqrt{2}}\right\rbrack\left\lbrack \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right\rbrack$

How do they perform this step given that they need to evaluate $f(x)$ but $|x\rangle$ is superposed? I know I could multiply everything out, apply $U_f$ to the basic states, and then rearrange to get the desired form, but is there a simpler way to see that second equation from the first one? I can get the following:

$|\phi_2\rangle = \left\lbrack\frac{(-1)^{f(x)}|0\rangle + (-1)^{f(x)}|1\rangle}{\sqrt{2}}\right\rbrack\left\lbrack \frac{|0\rangle - |1\rangle}{\sqrt{2}} \right\rbrack$

but then I am lost. Does it always amount to going to basic states and then returning to a more compact form or can I do something smarter?

Answer 1

The key point here is that the query oracle $U_f$ is a linear transformation.

Linearity means, if $|x\rangle = \alpha|0\rangle+\beta|1\rangle$, then

$$U_f|x\rangle|y\rangle=U_f(\alpha|0\rangle+\beta|1\rangle)|y\rangle=\alpha U_f|0\rangle|y\rangle+\beta U_f|1\rangle|y\rangle\,.\tag{1}$$

---

Now, we have $$U_f|x\rangle|y\rangle=|x\rangle|y \oplus f(x)\rangle\,,\tag{2}$$

and when $|x\rangle$ is either $|0\rangle$ or $|1\rangle$, and $y=|-\rangle$, we get

$$U_f|x\rangle|-\rangle=(-1)^{f(x)}|x\rangle|-\rangle\,.\tag{3}$$

So,

$$\begin{align}U_f\bigg[\frac{|0\rangle + |1\rangle}{\sqrt{2}}\bigg]|-\rangle &= \frac{1}{\sqrt{2}}U_f|0\rangle|-\rangle + \frac{1}{\sqrt{2}}U_f|1\rangle|-\rangle \tag{4.1}\\ &= \frac{(-1)^{f(0)}}{\sqrt{2}}|0\rangle|-\rangle + \frac{(-1)^{f(1)}}{\sqrt{2}}|1\rangle|-\rangle \tag{4.2}\\ &= \bigg[\frac{(-1)^{f(0)}|0\rangle + (-1)^{f(1)}|1\rangle}{\sqrt{2}}\bigg]|-\rangle\tag{4.3}\end{align}$$

Answer 2

Your misunderstanding is that $|x\rangle$ is only meant to denote either $|0\rangle$ or $|1\rangle$ -- not the superposition $H|0\rangle$. So $f(x)$ respectively denotes either $f(0)$ or $f(1)$, meaning that $f(x)$ is not evaluated in superposition. I agree the book is not totally clear on this point.

If you are looking for smarter way to think about this calculation, you can make more explicit use of the phase kickback as described here https://learning.quantum.ibm.com/course/fundamentals-of-quantum-algorithms/quantum-query-algorithms#further-remarks-on-the-phase-kickback

To support the idea that using the phase kickback really is an additional insight, note that Deutsch's original paper did not make use of the phase kickback. See here https://quantumcomputing.stackexchange.com/a/5397/27580 for more information.