I understand the following code on why the specific swaps take place, but when I try to replicate it with $N=35$, I get confused.
def c_amod15(a, x):
if a not in [2,4,7,8,11,13]:
raise ValueError("'a' must be 2,7,8,11,13")
U = QuantumCircuit(4)
for iteration in range(x):
if a in [2,13]:
U.swap(0,1)
U.swap(1,2)
U.swap(2,3)
if a in [7,8]:
U.swap(2,3)
U.swap(1,2)
U.swap(0,1)
if a == 11:
U.swap(1,3)
U.swap(0,2)
if a in [7,11,13]:
for q in range(4):
U.x(q)
U = U.to_gate()
U.name = "%i^%i mod 15" % (a, x)
c_U = U.control()
return c_U
for x in range(n):
exponent = 2**x
circuit.append(c_amod15(a, exponent),
[x] + list(range(n, n+m)))
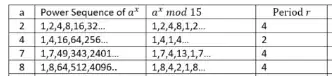
For example, if $a=8\,,$
- 0001 (start)
- (1st swap) 0010
- (2nd) 0100
- (3rd) 1000
- 2nd iteration = 0100
- 3rd iteration = 0010
- 4th iteration = 0001
This loops back to 1 with a period of 4.
When I try to repeat this with $N=35$ and, let's say, $a=8$, I get the following values.
1= 000001
8= 001000
29= 011101
22= 010110
The problem I'm having is I don't know how to loop through those numbers with just $SWAP$ and $X$ gates.