Inverse Quantum Fourier Transformation

Question

I have the exercise to implement the Inverse QFT with Qiskit for any number of qubits without the swapping part. I tried to implement something like this for any $n$.

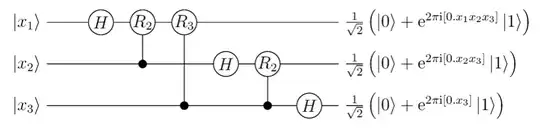
Now I got this code but it doesn't work and I'm kinda lost because I do not know if it's a mistake of the controlled Z-rotation (which we have to do using only Single Qubit Gates and CNOT) or if I misunderstood the inverse Fourier transformation and have to do something else.

    #Implementation of the inverse QFT
def inverse_QFT(n):
    qc = QuantumCircuit(n)
pi = np.pi
# do the rotations with for loops on the quantumregister q = (q[n-1],...,q[1],q[0])
for j in range(n-1,-1,-1):
     #Hadamard on the jth qubit
     qc.h(j)
     for k in range(j-1,-1,-1):
         # The Controlled Z Rotations by theta

        theta = 2*pi / (2**(j-k))
        qc.cx(j,k)
        qc.rz(-theta, j)
        qc.cx(j,k)
        qc.rz(theta, j)

return qc

I wanted to add, that the code does work (so I get an output) but does not give me the right answer.

Edit: I changed the exponent from $k$ to $j-k$. But it still does not work.

Answer 1

So I found out, that the Rz gate didn't do what I thought it did. I found another a way to represent the controlled phase gate with single qubit gates and CNOT over this Link https://physics.stackexchange.com/questions/213002/in-quantum-fourier-transform-why-can-any-controlled-r-k-gate-be-formed-by-t/213168#213168 So I changed the code to the following

        for j in range(n-1,-1,-1):
             #Hadamard on the jth qubit
             qc.h(j)
             p = 0
             for k in range(j):
                 p += 1
                 # controlled phase gate
                 #qc.cp(-pi/(2**(p)),j-k-1,j)
                 #single qubit and CNOT
                 theta = (2*pi/2**(p))           
                 qc.p(2*theta, j-k-1)
                 qc.p(2*theta, j)
                 qc.cx(j-k-1,j)
                 qc.p(-2*theta, j)
                 qc.cx(j-k-1,j)
       for k in range (int(n/2)):
           qc.swap(k, n-1-k)
   return qc

This works perfectly fine