I was following Surface code quantum computing by lattice surgery. A few questions about this paper have been asked in this forum, but I believe my question is new. The main text took a 'state picture' of what happens and in the appendix, the authors provides the stabilizer description. I want to ask specifically about the rough merge.
Just by the definition 'a rough merge measures $XX$ of two qubits, we can derive the quantum states after the merge, as in Eq.(3)
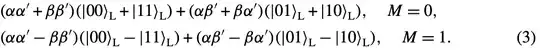
where $M$ is the measurement result, and the states of the qubits before the measurement are $|\psi\rangle=\alpha|0\rangle+\beta|1\rangle$ and $|\phi\rangle=\alpha'|0\rangle+\beta'|1\rangle$.
Then, by defining the basis states of the merged patch as Eq.(4)
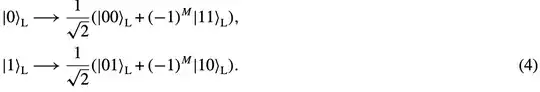
we can express rough merge in the state picture as Eq.(5)

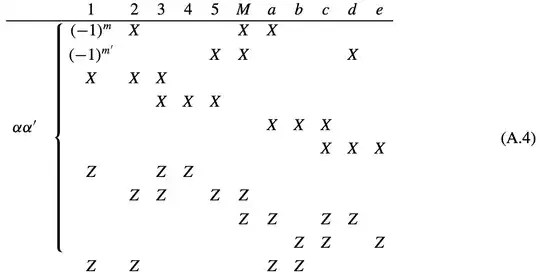
In the stabilizer description, I can follow the updates of stabilizer table, e.g. if we start from $|00\rangle$, we get this table in Eq.(A.4)
Eq.(6) is the superposition of four cases
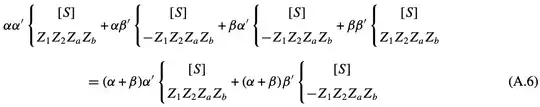
In this notation of a state, $[S]$ are the usual stabilizers in a surface code and additionally, the state is stabilized by the Pauli in the second line.
My first issue is that Eq.(A.6) has a typo? If we're factoring out the common terms, should the first and the fourth states be combined together since they have the same state? And the middle two terms should be combined together? This is not the same with what the authors do.
I think the correct result should be something like
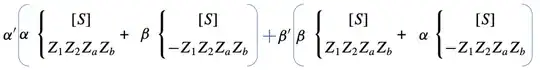
The next step is to map the states of the two qubits before to basis states of the merged patch.
This map is given in Eq.(4). And the authors got Eq.(A.7)
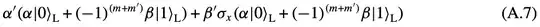
This is my second issue: I fail to see how we can get to Eq.(A.7) from Eq.(A.6) and Eq.(4). A state stabilized by $Z_1Z_2Z_aZ_b$ just means the parity of the two qubits are even, which can be anything in the span of $|00\rangle$ and $|11\rangle$? How does the sign before $\beta$ come about? Given a set of stabilizers, we don't know what the sign of the state is, or more generally, its phase.