Why is this modular adder so complicated?

Question

I'm trying to construct a controlled modular multiplication circuit and a subcomponent is a modular adder. However, it appears the basic Draper/Fourier adder is already modular. Shouldn't adding $N=2^n$ to $a$ cause the phase to multiplied by $exp(2\pi i (a+N))=exp(2\pi i a)$ in Fourier space, so you get the same result? I seem to be getting $a+b \, (mod N)$ for both my implementation and the Qiskit implementation of the Draper adder.

However, the circuit in the paper is much more complicated. He's adding $a$ based on the double control bits $c_1, c_2$, subtracting $N$, adding $N$ back if $a+b \ge N$ ... then subtracting $a$ based on the double control bits $c_1, c_2$ then ... I kind of lost the thread at this point.

Answer 1

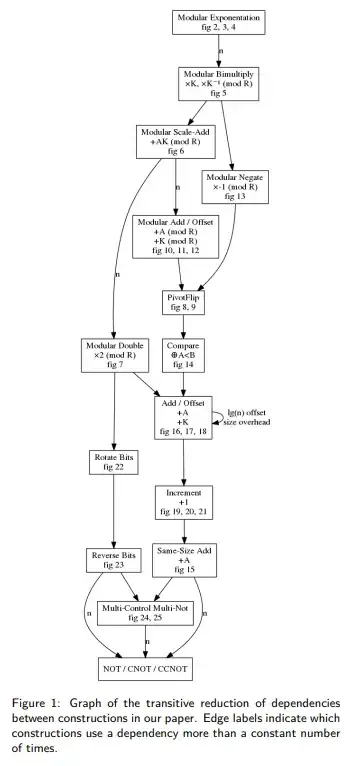
Shouldn't adding $N=2^n$ to $a$ cause the phase to multiplied by $exp(2\pi i (a+N))=exp(2\pi i a)$ in Fourier space, so you get the same result?

Right, if $N$ is a power of 2, you don't need a modular adder circuit. You just use a normal adder circuit. This is true of all inplace adder circuits, not just the Draper adder circuit.

Sometimes people call normal adder circuits "modular adder circuits", distinguishing them from circuits where the number of output bits is larger than the number of input bits so that there is never an overflow. I don't really like that naming, since it's not reflective of what's cheap vs what's expensive.

the circuit in the paper is much more complicated

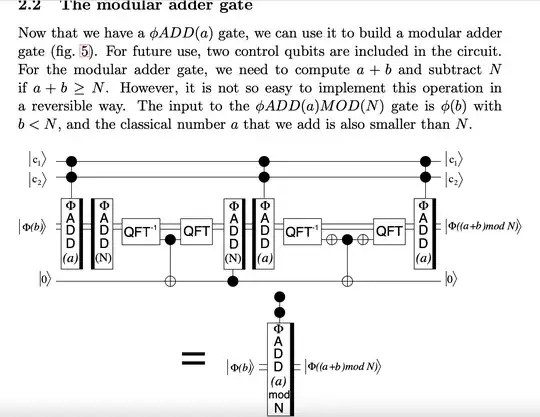
The circuit in the paper is for working mod $N$ where $N$ isn't a power of 2, such as for Shor's algorithm. So it can't just use a normal adder.

Effectively, the circuit is doing this:

# decomposition of a += b (mod N)
a += b
let tmp = (a >= N)
if tmp:
    a -= N
del tmp = (a < b)

but with some controls on key operations that ensure nothing happens if the controls are OFF, and with the comparison operations decomposed into checking whether an addition or subtraction overflows.

---

Note that the paper "Factoring with n+2 clean qubits and n-1 dirty qubits " has diagrams and working code implementing modular multiplications. The constructions are a bit convoluted because they go out of their way to use minimal workspace, but they are also built entirely out of classical gets (NOT, CNOT, TOFFOLI); no Hadamards or Fourier transforms. That makes them easier to check.

Answer 2

The thing is that Drapers QFT-based adder (as well as in other implementations of adder circuits) is modular for $N=2^{n}$ if the number of qubits in the register which carries the result is $n$. The circuit in the drawing is taken from Beauregard's paper here which implements modular adder for general $N$ (where the addends $a$ and $b$ are smaller than $N$). In the paper Beauregard Implements Shor's algorithm therefore addition (and multiplication and exponentiation) modulo $N$ for general $N$ are required.

The circuit works as follows, first a constant $a$ (which is not carried by a register but coded into the phases in Drapers adder) is added to register $b$ (carrying number $b$). Then $N$ is subtracted from register $b$ and re-added to register $b$ if $a+b < N$ (this is done by checking the most significant bit of register $b$ in the 'regular' basis - the QFT's in the circuits are required to move out and back into the Fourier basis). The purpose of the last part of the circuit (the sub-circuit which includes the last two adders) is to disentangle an auxiliary qubit (the bottom qubit in the drawing) from register $b$ which carries the result. At the output this auxiliary qubit is in the state $|0 \rangle$ and can be reused.

The two control qubits (the top qubits) have no role in implementing modular addition -- they are required for implementing modular multiplication and exponentiation in the general Shor's circuit (in Shor's circuit one control belongs to the register that carries the number we wish to multiply and the other belongs to the register that carries the power in exponentiation).

In Classiq's library git-repo you can find full implementations of Modular addition, multiplication, exponentiation and Shor's circuits similar to Beauregard's paper (excluding the fact that the exponentiation and Shor are implemented on a full $2n$ register and do not use the 'one controlling qubit trick' as in the paper) Shor - Classiq Library (Disclaimer - I am a Classiq employee)