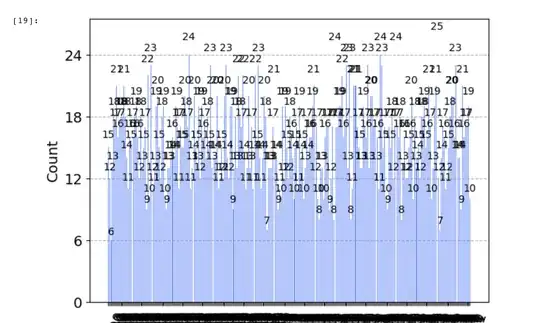
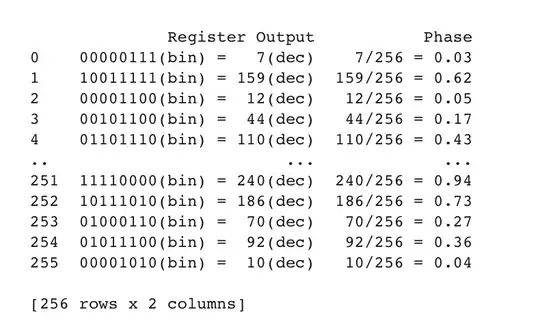
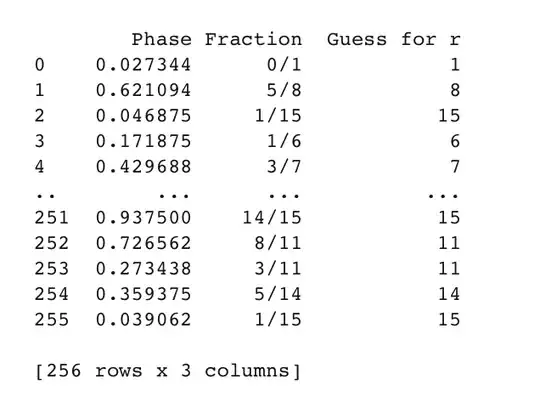
I have implemented Shor's algorithm for $N=15$ from this tutorial. I understand the algorithm pretty well, but I'm a little confused at the output I'm getting from running the circuit. It appears to be all over the place. The function $\text{qpe_amod15}$ seems to take the zero-th reading and use that phase and extracted period, which has resulted in successful factorizations so far.
Does this look normal or am I just getting lucky?
 ]
]