All the references on Grover / Amplitude Amplification (AA) (Mike&Ike, wiki, Lin Lin lecture notes, etc.) give a recipe for preparing the desired state (or amplifying the state) with probability $\gamma=O(1)$. Can one improve this result by provably making the success probability exponentially close to 1? (At the cost of the polynomial increase of the algorithm cost.)
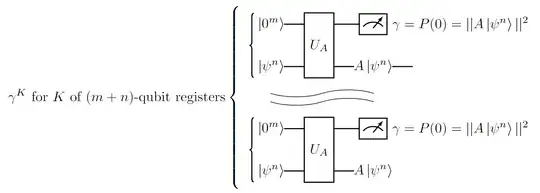
My question is motivated by the following construction (see the circuit below). Imagine that one needs to do Grover / AA on $K$ parallel registers. If the success probability is $\gamma$ for each register, the total success probability is $\gamma^K$, which is not scalable with $K$ (assuming that the number of qubits $m+n$ in each register is fixed), unless there is a way to make $\gamma$ itself exponentially close to $1$.
Note that if $A$ is unitary (as in the case of using QSP for simulating time evolution), then one can indeed make $\gamma$ exponentially small at a cost polylogarithmic in problem parameters. However, for $A$ being non-unitary one would need to first somehow amplify each $\gamma$.