I would like to precisely understand why we need to decode syndrome "live" when we want to perform $T$ gates. For this reason I consider different scenario (some are fictive but helpful to understand the physics) in order to understand which exact ingredient imply that a "live decoding" is necessary. The questions related to these scenario are labelled as Q1,Q2,Q3 below.
Scenario I: Clifford only circuit at the physical level: I can decode "later"
Assuming I only have physical Clifford gates (and preparation and measurements are in some Pauli basis), I know that I can easily keep track of physical Pauli errors through my circuit (Gottesman Knill theorem). So for an error corrected circuit only composed of Clifford gates at the physical level, I can simply keep in memory the syndromes that occured along my computation as well as the final Pauli measurements. Through classical post-processing (which could occur after my quantum computation has been done), I could deduce how to re-interpret the final measurements so that the correct outcome occured. A live decoding is un-necessary in this case.
Q1: do you agree with this paragraph?
Scenario II: Clifford+T circuit through state injection: I "usually" need to decode live
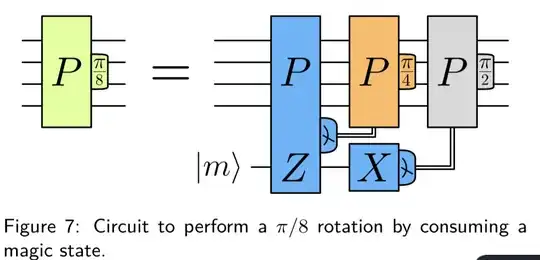
Consider the following state injection protocol:
Case I: I want to perform the classical corrections "on the spot"
In order to know which classically controlled correction I should apply before the next gate (the $\exp(-i P \pi/4)$ or $\exp(-i P \pi/2)$), I obviously need to have have decoded the syndrome before the next gate. Clearly in this case the decoder must keep up with the computation speed "live".
Case II: I want to perform the classical correction "later".
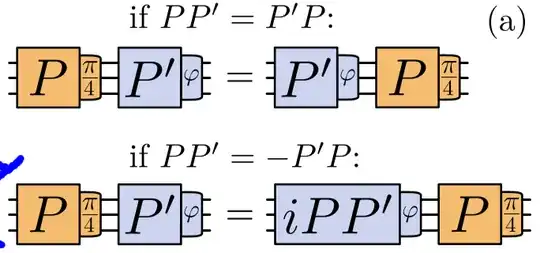
Because $\exp(-i P \pi/4)$ and $\exp(-i P \pi/2)$ are Clifford, I can commute them toward the end of the circuit. So in principle I could delay my correction and have more time to decode. However, when I do this procedure, the following $T$-gate might be modified as indicated on the following image (case $PP'=-P'P$). Because of that, I actually have no choice but to decode "on the spot" (otherwise I will not do the following $T$-gate I am supposed to do). Q2: Am I correct in this paragraph?
Now, imagine a fictive algorithm in which all the $T$-gate occurring later in my circuit commute with the Clifford correction I need to apply (case $PP'=P'P$). In this case, couldn't I run my quantum algorithm, keep track in a classical memory of all the syndromes and final measurements. Then after my quantum algorithm is done, I use a classical algorithm to deduce how my final measurements should be re-interpreted. In this case I think it would work because the "good" final measurement would only differ by a Clifford correction from the one I actually observed: Gottesman Knill would be applicable. Overall, a live decoding would be un-necessary here. Q3: Am I correct in this paragraph?