I am trying to understand the math behind the following applications of gates on three qubits:
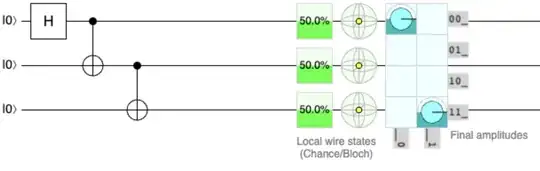
You can view this via the Quirk simulator here:
What I have so far is the following:
(1) The first qubit begins in state
$ \begin{bmatrix} 1 \\ 0 \end{bmatrix} $
Any applying Hadamard gives:
$ \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \times \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} $
(2) The next step is to apply the CNOT gate to the first two qubits. I compute the tensor produce of the states of the first two qubits in the following way:
$ \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \end{bmatrix} $
Then, apply CNOT:
$ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \end{bmatrix} $
Now I have the first two qubits in an entangled state.
(3) In step three, I need to apply the CNOT gate to the second and third qubits. This is where I am unsure the correct way to do the math. I cannot just multiple the second and third qubits by the regular CNOT matrix independently, because the first and second qubits are entangled. One guess is that I need to create the state vector representing all three qubits:
$ \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \end{bmatrix} $
(NOTE: I edited the math above. When the question was initially posted it had the wrong result for the tensor product.)
What is the proper matrix to multiply this by? What is the technique to construct a version of the CNOT gate that will work for this length-8 state vector with two qubits already entangled?
Thanks.