Output of my quantum circuit to create 3-qubit GHZ-like state does not make sense mathematically

Question

I want to create the GHZ-like state, $|\Psi\rangle = \frac{1}{\sqrt{2}} \left(|011\rangle - |100 \rangle \right)$. I build my circuit in the following way.

1. apply the x gate to the first and third qubits to make the input as $|101\rangle$
2. apply the Hadamard gate to the first qubit
3. apply the CNOT gate to (q0,q1) and (q1, q2)

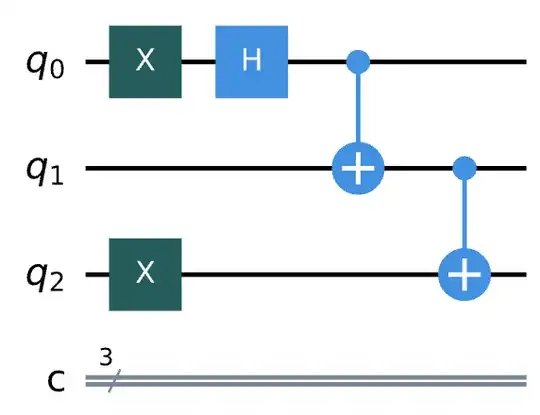
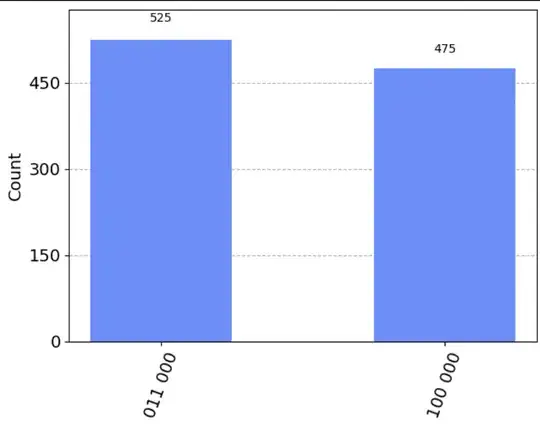
I run the simulation to make sure that I get the right reult. However, I failed to get the expected state mathematically. Here is how I do the calculation:

$(H\otimes I \otimes I)|101\rangle = H|1\rangle \otimes I|0\rangle \otimes I|1\rangle = \frac{1}{\sqrt 2} (|0\rangle - |1\rangle) \otimes |0\rangle \otimes|1\rangle = \frac{1}{\sqrt 2} (|001\rangle - |101\rangle)$

Apply CNOT gates: $\frac{1}{\sqrt 2} (|001\rangle - |101\rangle) \rightarrow \frac{1}{\sqrt 2} (|001\rangle - |111\rangle) \frac{1}{\sqrt 2} (|001\rangle - |110\rangle)$

My calculation tells me I should input $|110\rangle$ instead : $(H\otimes I \otimes I)|110\rangle = H|1\rangle \otimes I|1\rangle \otimes I|0\rangle = \frac{1}{\sqrt 2} (|0\rangle - |1\rangle) \otimes |1\rangle \otimes0\rangle = \frac{1}{\sqrt 2} (|010\rangle - |110\rangle)$

Apply CNOT gates: $\frac{1}{\sqrt 2} (|010\rangle - |110\rangle) \rightarrow \frac{1}{\sqrt 2} (|010\rangle - |100\rangle) \frac{1}{\sqrt 2} (|011\rangle - |100\rangle)$

Could anyone tell me what's wrong with my calculation?

Answer 1

As @Callum said, your ordering of qubit is wrong. Qiskit keeps the 0th qubit at the rightmost space in a ket representation or for measurement.

If you have, say 3 qubits, qubit#1, qubit#2, qubit#3, in state $|-\rangle_1$,$|1\rangle_2$ and $|+\rangle_3$, respectively, then their joint state is written as $|+_31_2-_1\rangle$ i.e, $|+1-\rangle_{3,2,1}$, where subscript denotes the qubit number for the corresponding state.

For your circuit, state progression will go as follows:

• Your initial state will be $|000\rangle_{3,2,1}$

• Applying $X_1$ will get you $|001\rangle_{3,2,1}$

• Applying $X_3$ to that state will get you $|101\rangle_{3,2,1}$.

I hope the qubit ordering is clear now.

---

As you have asked in your comment, yes, even if $|101\rangle$ is a "symmetric state" as you have said, Applying $H_3$ will give you $|001\rangle - |101\rangle$ and applying $H_1$ will give you $|100\rangle - |101\rangle$.

---

Now, for your circuit, the state will evolve as follows:

$$|000\rangle \xrightarrow{X_1X_3} |101\rangle \xrightarrow{H_1} \frac{|100\rangle-|101\rangle}{\sqrt{2}} \xrightarrow{CNOT_{1\rightarrow2}}\frac{|100\rangle-|111\rangle}{\sqrt{2}} \xrightarrow{CNOT_{2\rightarrow3}}\frac{|100\rangle-|011\rangle}{\sqrt{2}}\,,$$

thus, giving you the histogram you have pasted in the question.