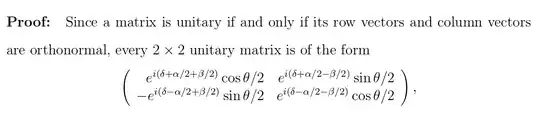On unitary matrix form suggested in the Elementary gates paper

Question

In the "Elementary gates for quantum computation" paper Barenco et al. start their proofs by defining a generic form of $2\times 2$ unitary matrices as follows:

Can you help me with the basic arithmetic behind this statement? For unitary matrix $\begin{bmatrix}a & b \\ c & d\end{bmatrix}$ do we expect $ab + cd = 0$ ? Is this property really satisfied in this case?

Update Indeed! My confusion came from the incorrect treatment of inner products. As suggested below, the correct invariant is $\overline{a}b + \overline{c}d = 0$

Answer 1

For a matrix to be unitary, you require $UU^\dagger=I$. Thus, $$ \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} a^\star & c^\star \\ b^\star & d^\star \end{bmatrix}=\begin{bmatrix} |a|^2+|b|^2 & ac^\star+bd^\star \\ a^\star c+b^\star d& |c|^2+|d|^2 \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $$ The diagonal elements tell you that the rows must both have length 1. The off-diagonal elements both give the same information: that the two rows must be orthogonal to each other. Unlike what you stated in the question, that means you have to remember to take the Hermitian conjugate of one row.