Does subtraction circuit have a class like full or half Carry adder circuit in qiskit? one subtraction circuit code-example in qiskit?

Question

I need a subtraction circuit to calculate Laplacian in edge processing, but I didn't find any class in qiskit.Do I have to write the code myself?

Answer 1

For subtraction as mentioned earlier you have to negate the number, and than use an adder.

There are few possible implementations for that (adder can be with QFT or with ripple-carry adder with more or less auxiliaries)

Once you use a high-level compiler, you can subtract without the low-level implementation.

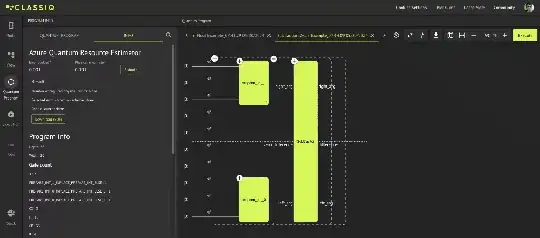
You can use the classiq compiler with the following code from this git repo. Also, using different optimization parameters for the compiler will automatically choose the implementation. Regarding the representation of the sign, once the variable is defined as a signed number using QNum[3, True, 1] (True for signed number) you can use the executor to interpret it correctly.

Here is an example:

from classiq import *
@qfunc
def main(a: Output[QNum[3, True,2]], b: Output[QNum[4,False,1]], res: Output[QNum]) -> None:
    allocate(3, a)
    allocate(4, b)
    hadamard_transform(a)
    hadamard_transform(b)
res |= a-b


qmod = create_model(main)
qprog = synthesize(qmod)
show(qprog)
job = execute(qprog)
result = job.result()[0].value
print(result.parsed_counts)
job.open_in_ide()

You can see how to interpret the results in the IDE at platform.classiq.io or in Python according to the answer here

If you need the qiskit circuit object of, use this command to get the QASM:

QuantumProgram.parse_raw(qprog).transpiled_circuit.qasm

And convert it with the answer here

Disclaimer - I am an engineer at Classiq

Answer 2

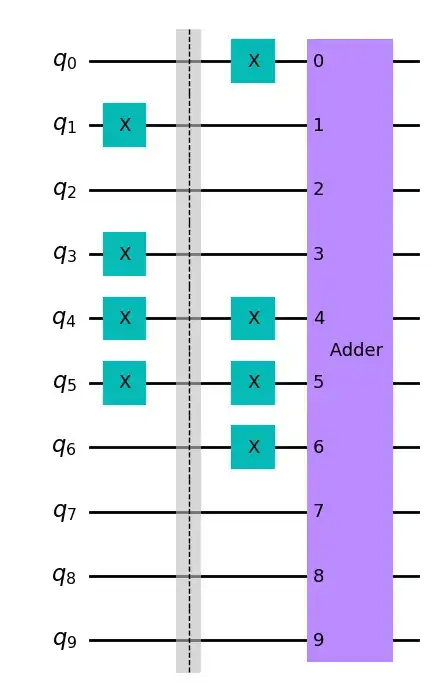
A full-adder circuit can be used for subtraction by using the fact that: $$a - b = a + \neg b + 1$$ So, you need to invert the subtrahend, increment it by one, then do the addition as usual. As an example, the following code uses VBERippleCarryAdder to subtract 3 from 5:

from qiskit import QuantumCircuit
from qiskit.circuit.library import VBERippleCarryAdder
num_state_qubits = 3
adder = VBERippleCarryAdder(num_state_qubits, name=' Adder ')
num_qubits = len(adder.qubits)
circ = QuantumCircuit(num_qubits)
Five
circ.x([1, 3])
Three
circ.x([num_state_qubits + 1, num_state_qubits + 2])
circ.barrier()
Subtraction:
1) invert b:
circ.x(range(num_state_qubits + 1, 2 * num_state_qubits + 1))
2) add one (using carry-in)
circ.x(0)
3) do the addition
circ.append(adder, range(num_qubits))
circ.draw('mpl')

If you run this circuit the output will be: $001{\color{red}0\color{red}1\color{red}0}1011$