For transparency, I also posted this at the physics stackexchange, but it might be more fruitful to discuss here.
Already in the original transmon paper by Koch et al. is it stated that while the coupling of the transmon to an external magnetic flux bias allows for an in situ tuning of the Josephson coupling energy, it also opens up additional channels for energy relaxation.
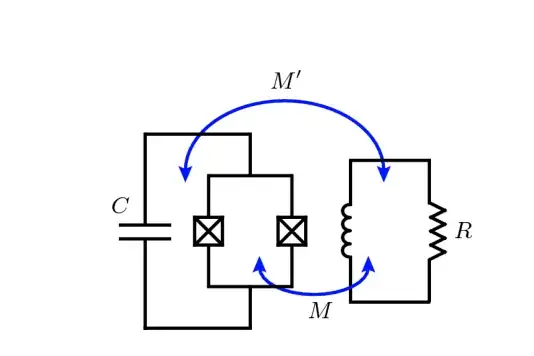
The paper then goes on to say that this loss occurs via the desired mutual inductance $M$ between the SQUID loop and the flux bias line, as well as via an undesired mutual inductance $M'$ between the whole transmon and the flux bias line. Some estimates are made, but in particularly no way to properly estimate or simulate the latter is given. In my opinion there should also be a (stray) capacitance term but they do not include it.
The effective circuit they give is shown here
An actual image of the FBL next to the SQUID is as follows
My question is how to do accurately calculate/simulate the actual losses into a FBL. In Concentric transmon qubit featuring fast tunability and an anisotropic magnetic dipole moment by Braumuller et al. some initial calculations are made, which I think are done assuming that the transmon is an LC circuit coupled to a 50 Ohm loss channel either capacitively or inductively. Specifically, at the top of page 3 they estimate $\Gamma_{1,ind} = \omega_q^2 M^2 /L Z_0$ and $\Gamma_{1,cap} = \omega_q^2 C_c^2 Z_0^2/C$, where $\omega_q$ is the transmon frequency, $M$ is the aforementioned mutual inductance, $L$ is the transmon (effective) inductance, $C$ is the transmon capacitance, $Z_0$ is the impedance of the FBL, and $C_c$ is the capacitance to the FBL.
However, in this calculation it seems to me that either $M$ or $M'$ is ignored (I assume the latter). Furthermore there are no transition matrix elements involved. And while that is obviously more complicated in any case, the impedance of the flux bias line is assumed to be frequency independent, while in practice there might be a filter involved, there might be a non-flat power spectral density, thermal excitations..
Does anyone know of references that go beyond this simple LC oscillator model? I have not been able to find them.
Edit: I found out that https://scqubits.readthedocs.io/en/latest/_generated/scqubits.TunableTransmon.t1_flux_bias_line.html#scqubits.TunableTransmon.t1_flux_bias_line takes care of the $M$ term, precisely implementing it using matrix elements as desired. But I am still not sure how one would estimate the $M'$ term, or the missing capacitive term for that matter.