Entangling two particles at a distance

Question

Entangled quantum particles are very interesting as they only make sense if you look only at the math.

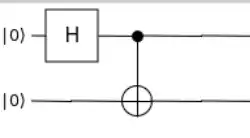
Usually, when we talk of "entangling" two qubits, we mean that we have two qubits, $A$ and $B$, both initialized in the $| 0 \rangle$ state. We then run this circuit on them:

This puts the system into the state $\frac{1}{\sqrt2} | 00 \rangle + \frac{1}{\sqrt2} | 11 \rangle$.

This circuit only works when the two qubits can be used together in a single circuit. Is there any way to entangle two qubits together (like this) at a distance? I guess it may require having a quantum circuit able to work between distant qubits; something that may be impossible.

Answer 1

The whole point of entanglement being something interesting to study is that entanglement cannot be created at a distance. This is essentially by definition: separable states are the states that we can create between two parties without quantum communication. Entangled states are the states that are not separable. Therefore, they require quantum communication.

Hence, entanglement is a resource that you have to generate by some awkward mechanism but, once you have it, it gives you the capacity to achieve feats that you wouldn't be able to without it.

You have to have some sort of local interaction between the qubits in order to generate the entanglement. That is typically either one party sends a qubit to the other party (with some controlled-nots etc performed by just one party) or, there is some source between the two parties spitting out entangled qubits (e.g. entangled photons via a process such as parametric down conversion).