I've only recently, and still only haphazardly and rather poorly, begun to understand Ising models with local interactions. I'm interested in particular in the simple one-dimensional Ising model with nearest and next-nearest neighbor interactions, which have been referred to in the literature as ANNNI Hamiltonians, or anisotropic, next-nearest neighbor interactions (with none, either, or both a transverse and longitudinal external magnetic field).
Depending on the strengths of the nearest-neighbor interactions relative to the next-nearest neighbor interactions (and also to the external magnetic fields) there could be very lovely and dynamic frustration going on - the nearest neighbor might favor parallel spins $\mid\uparrow\uparrow\rangle$ or $\mid\downarrow\downarrow\rangle$ but the next-nearest neighbor interactions might force antiparallel spins $\mid\downarrow\uparrow\rangle$ or $\mid\uparrow\downarrow\rangle$, or vice-versa.
- Can we say anything about if and when frustration leads to an entangled ground state?
The answer might be related to so-called area laws, which consider the amount of entanglement relative to the dimension of the chain. For a one-dimensional chain an area law suggests that there may be little entanglement, but is there any additional entanglement borne out of frustration?
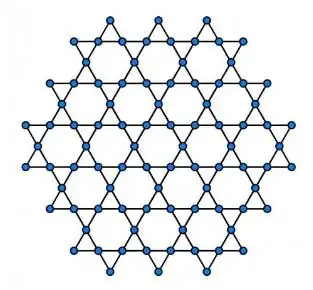
This was also partly inspired by Sandy Irani's presentation at the Israeli Institute for Advanced Studies here, where she mentions frustration in the context of a Kagome lattice.
I gathered from her talk that the Kagome lattice puts some stress on naive implementations of classical many-body algorithms like DMRG, but nonetheless from clever DMRG simulations there's some evidence that the lattice does indeed have a uniquely quantum (non-degenerate and highly entangled) ground state.