I'm learning the Swap Test, a quantum circuit to calculate the inner product of two quantum states $|\langle \phi|\psi\rangle|^2 $:
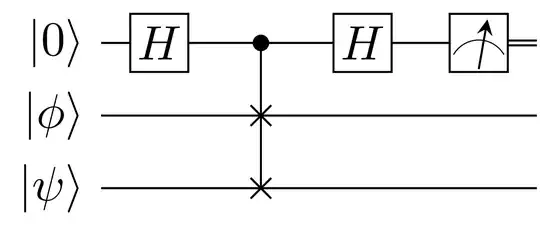
For the error analysis of this quantum circuit, according to Swap Test:
"This allows one to, for example, estimate the squared inner product between the two states, $|\langle \phi|\psi\rangle|^2 $, to $\epsilon$ additive error by taking the average over $O(\frac {1}{\varepsilon ^{2}})$ runs of the swap test."
What's the "additive error $\epsilon$ " from a statistical point of view? Is it MSE, RMSE, or Variance? Can RMSE serve as an additive error of the Swap Test?