I found this question while looking for something else but couldn't resist it. It was fun.
Yes, for any n >= 3, you can approximate any n qubit unitary to arbitrary accuracy with n qubits and the only allowed quantum gates being Clifford+Toffoli.
As already noted, for n < 3 you need 3 qubits to get anything non-Clifford because the Toffoli is a 3 qubit gate.
This is assuming you're okay with mid circuit measurement and reset.
Then you can deterministically implement the CS gate with the following 3 qubit Clifford+Toffoli circuit (from the legitly free to read online Picturing Quantum Software textbook at https://github.com/zxcalc/book)
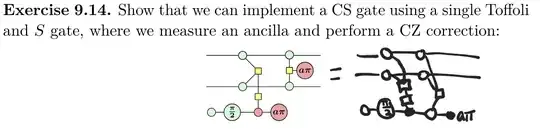 This textbook circuit classically conditions the CZ on the outcome of that mid-circuit single qubit measurement.
Another option is I drew how to do it without feedforward by instead doing one more CCZ gate.
This textbook circuit classically conditions the CZ on the outcome of that mid-circuit single qubit measurement.
Another option is I drew how to do it without feedforward by instead doing one more CCZ gate.
Then if I understood the paper at https://www.nature.com/articles/s41534-021-00424-z, you can approximate any 2 qubit unitary by a 2 qubit Clifford+CS circuit, and from our circuit above that is deterministically implementable as a 3 qubit Clifford+Toffoli circuit.
This includes 2 qubit unitaries of the form any single qubit unitary tensor identity, so you can approximate any single qubit unitary with an irrelevant borrowed ancilla - it is irrelevant because you need 3 qubits to do a Toffoli in the first place.
So you can then approximate any n qubit unitary where n >= 3 with an n qubit Clifford+Toffoli circuit where mid circuit measurement and reset are allowed. The easiest argument for this is because you can approximate Clifford + any non-Clifford single qubit unitary such as T without ancilla.
Fun fact: for qudits of odd prime dimension, you can get a single qudit non-Clifford gate (with some number of borrowed ancillae: it's 2 for qutrits) unitarily with the (3-qudit) Toffoli + Hadamard gate set: the gate that is identity on all computational basis states except for say, the last one. For instance for qutrits the matrix is diag(1,1,-1). But this trick is no good for qubits as diag(1,-1) is the very much Clifford Z gate.
So I don't know if it's possible to unitarily get a single qubit non-Clifford gate from Toffoli+Hadamard (seems not so plausible) or Clifford+Toffoli (I don't know). Maybe someone has proved this before, I don't know. Curious. An obvious thing to try for Clifford+Toffoli is to see if there's some modification of the above hand drawn circuit with more compute-uncompute tricks, so you need only borrowed ancilla(e?).
