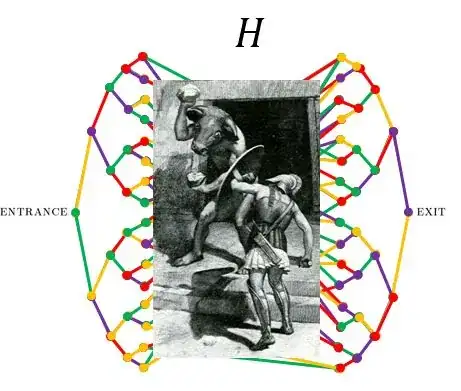
Reviewing Childs, Cleve, Deotto, Farhi, Gutmann, and Spielman's famous 2002 welded-trees problem, a quantum Theseus can find his way out of a labyrinth having an exponential number of rooms (vertices), with each room other than the entrance and exit having three doors with small hallways (edges) connecting to other rooms. Theseus can dispense of the classical Minotaur who had been stuck endlessly running around the middle of the maze; Theseus himself can tunnel through this central portion to escape and doesn't need to use Ariadne's trick of tying a string to the entrance to trace his way back. Indeed, I learned recently that Theseus shouldn't tie a string to the entrance, because in order to get out of the maze he needs to forget his path from whence he came!
Nonetheless the paper of Childs et al. describes a Hamiltonian simulation or a quantum walk based on edge-coloring - which I interpret as if each of the doors and hallways in the maze are one of a number of different colors. The paper describes how to efficiently and randomly choose nine different colors $c\in\{A,B,C\}\times\{1,2,3\}$ for the hallways, but below I use four colors $c\in\{\mathrm{\color{#FFBF00}{YELLOW},\color{#008000}{GREEN},\color{#BB3385}{PURPLE},\color{\red}{RED}}\}$ for convenience:
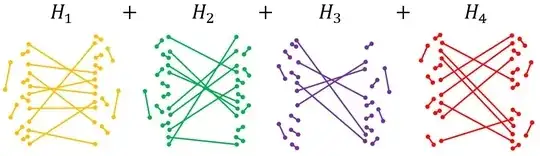
But, how does this edge-coloring help in the quantum walk? Could the adjacency matrix $H$, which is necessarily Hermitian as it's a symmetric $(0,1)$ matrix, be decomposed into a sum of four different Hermitian matrices $H=H_1+H_2+H_3+H_4$?
That is, could we Trotterize to simulate:
$$e^{-iHt}=e^{-i(H_4+H_3+H_2+H_1)t}\approx \big (e^{-iH_4t/r}e^{-iH_3t/r}e^{-iH_2t/r}e^{-iH_1t/r}\big)^r$$
by repeatedly doing:
- a little bit of SWAP'ing on Theseus's position for rooms connected by yellow hallways with $e^{-iH_1/r}$, then
- a little bit of SWAP'ing Theseus's position for rooms by green hallways with $e^{-iH_2/r}$, then
- a little bit of SWAP'ing for rooms connected by purple hallways with $e^{-iH_3/r}$, then
- a little bit of SWAP'ing for rooms connected by red hallways with $e^{-iH_4/r}$?
If so, how does the oracle that colors the hallways or edges help out? For example do we calculate and store the color of each edge in an ancilla and only do the SWAP'ing conditioned on the value of the ancilla, making sure to uncompute along the way?