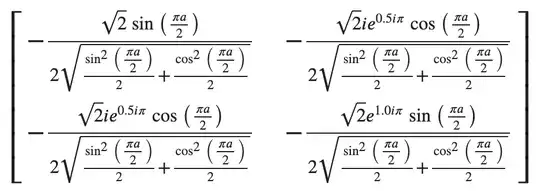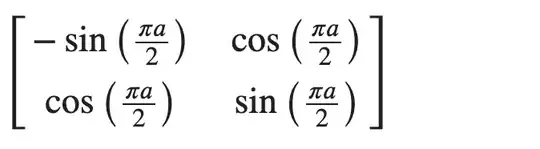0

For a very simple circuit, such as

from pytket.circuit import Circuit, fresh_symbol

a = fresh_symbol("a")
circ = Circuit(1)
circ.X(0)
circ.Ry(a,0)

the circuit that results from applying a SquashTK1 pass:

from pytket import passes

passes.SquashTk1().apply(circ)

has a very complicated expression for it's parameters:

$$ -2 \operatorname{atan}_2\left(-\frac{\sqrt{2} \cos \left(\frac{a}{2}\right)}{2},-\frac{\sqrt{2} \sin \left(\frac{a}{2}\right)}{2}\right). $$

In the end, this expression is the arctan of a tan and it may be used as a replacement of taking the modulus, but I wonder if anyone has any idea why this occurs.

Callum
  • 1,260
  • 1
  • 5
  • 24
Diego Olvera
  • 1

1 Answers1

1

Squashing symbolic gates with optimisation passes like SquashTK1 frequently leads to lengthy trigometric expresions. See the pytket user manual for some background.

However in this case its possible to simplify the symbolic unitary with sympy.simplify.

from pytket.circuit import Circuit, fresh_symbol
from pytket.utils.symbolic import circuit_to_symbolic_unitary
from pytket import passes

a = fresh_symbol("a")
circ = Circuit(1)
circ.X(0)
circ.Ry(a, 0)


passes.SquashTK1().apply(circ) # squash two gates to a single TK1 gate


circuit_to_symbolic_unitary(circ) # view complicated unitary

The output looks like this

enter image description here

However we can make this look much nicer.

from sympy import simplify

simplify(circuit_to_symbolic_unitary(circ))

We get the simplier matrix below

enter image description here

I hope this helps. Let me know if this answers your question.

Callum
  • 1,260
  • 1
  • 5
  • 24