How to transform an Hamiltonian operator to a controlled gate (Hadamard test) in Pennylane?

Question

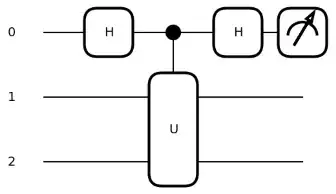
I would like to perform an Hadamard test on a given Hamiltonian operator $\hat{H}$ acting on a 2-qubits system. For instance, suppose $\hat{H}$ can be decomposed into a qml.PauliX on the first wire and a qml.PauliZ on the second wire, and it could be created in Pennylane by H = qml.Hamiltonian(qml.PauliX(0) @ qml.PauliZ(1)) and measured by returning qml.expval(H).

But because I would like to perform the Hadamard test, I need to transform the Hamiltonian into a controlled gate in the circuit: how can I do it in Pennylane?

score 1 · Answer 1 · answered Feb 23 '23 at 14:31

Given the 2-qubits Hamiltonian $\hat{H}$, this is how you can perform the Hadamard test in Pennylane:

import pennylane as qml
dev = qml.device('default.qubit', wires=3)
@qml.qnode(dev)
def hadamard_test(U):
    qml.Hadamard(0)
    qml.ControlledQubitUnitary(U.matrix(), control_wires=[0], wires=[1,2])
    qml.Hadamard(0)
    return qml.expval(qml.PauliZ(0))
ham = qml.PauliX(0) @ qml.PauliZ(1)
res = hadamard_test(U=ham)
qml.draw_mpl(hadamard_test)(U=ham)

More in general, you can transform any unitary matrix $U$ in a multi-controlled gate by using ControlledQubitUnitary.

score 0 · Answer 2 · edited Feb 24 '23 at 06:40

Isn't that just applying X and Z operators separately? For instance, if I compute it by hand:

op = np.matrix(qml.matrix(qml.PauliX(0)@qml.PauliZ(1)))
state = np.matrix([1,0,0,0])
state @ op.H
# matrix([[0, 0, 1, 0]])

which is exactly the same if I separately apply X and Z gates to my circuit i.e.

@qml.qnode(qml.device("default.qubit", wires=2))
def circuit():
    qml.PauliX(0)
    qml.PauliZ(1)
    return qml.state()
circuit()
# tensor([ 0.+0.j, -0.+0.j,  1.+0.j, -0.+0.j], requires_grad=True)

Otherwise, you can also use qml.PauliRot(theta, "XZ", wires=[0,1]) function and adjust the rotation angle accordingly.

How to transform an Hamiltonian operator to a controlled gate (Hadamard test) in Pennylane?

2 Answers2