This partial answer breaks the question of the closure of the levels of the Clifford hierarchy under inversion into two parts: the easy question of closure under complex conjugation and the harder question of closure under transposition. It also offers a proof of the former and an informal argument for the latter.
Lemma 1 (Every level of the Clifford hierarchy is closed under complex conjugation)
For every $k\geqslant 1$, we have
$$U\in\mathcal{C}^{(k)}\iff\overline{U}\in\mathcal{C}^{(k)}.\tag1$$
Proof. Equivalence $(1)$ is obviously true for every $U$ in the Pauli group $\mathcal{C}^{(1)}$. Assume that $(1)$ holds for $k$ and let $U\in\mathcal{C}^{(k+1)}$ and $P\in\mathcal{C}^{(1)}$. By definition $UPU^\dagger=V\in\mathcal{C}^{(k)}$. But then
$$
\overline{U}P\overline{U}^\dagger=\pm \overline{U}\overline{P}\overline{U}^\dagger=\pm\overline{(UPU^\dagger)}=\pm\overline{V}\in\mathcal{C}^{(k)}\tag2
$$
so $\overline{U}\in\mathcal{C}^{(k+1)}$. $\square$
This immediately gives us
Corollary 2 (Symmetric subset of every level is closed under inversion)
If $U=e^{i\theta}U^T$ for some $\theta\in[0,2\pi)$, then
$$U\in\mathcal{C}^{(k)}\iff U^\dagger\in\mathcal{C}^{(k)}\tag3$$
for every $k\geqslant 1$.
This provides a simple alternative route to closure under inversion for diagonal gates and extends it to gates such as $\sqrt{\text{iSWAP}}$ and various other swap gates. In fact, $(3)$ applies to every gate whose Pauli expansion consists of terms for which the parity of the number of $Y$ operators is the same (either all even or all odd). Unfortunately, this set does not include all permutations.
Conjecture 3 (Every level is closed under transposition)
For every $k\geqslant 1$, we have
$$U\in\mathcal{C}^{(k)}\iff U^T\in\mathcal{C}^{(k)}\tag4.$$
Informal argument. Clifford hierarchy arises as the set of gates that admit fault-tolerant implementation using gate teleportation, see page $3$ in "Quantum teleportation is a universal computational primitive". The protocol is summarized in figure $2$ of the paper
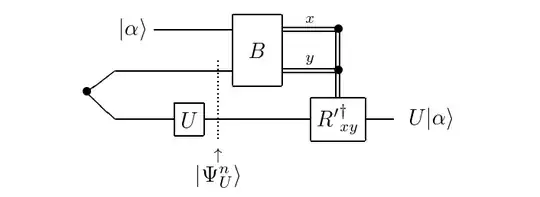
The protocol consists of two stages. In the first stage, we prepare $n$ Bell pairs $|\Phi^n\rangle$ and apply the desired gate $U\in\mathcal{C}^{(k)}$ to one half of the Bell pairs obtaining
$$
|\Psi^n_U\rangle=(I\otimes U)|\Psi^n\rangle.\tag5
$$
In the second stage, we perform Bell measurements $B$ on the input state $|\alpha\rangle$ and the other half of the state created in $(5)$ and finally apply corrections conditioned on the measurement outcomes using $R'^\dagger_{xz}\in\mathcal{C}^{(k-1)}$.
Now, it is easy to check that
$$
|\Psi^n_U\rangle=(U^T\otimes I)|\Psi^n\rangle.\tag6
$$
Thus, two changes are needed in the protocol above to effect $U^T$ rather than $U$. First, we can apply $U$ on the middle qubit rather than the bottom qubit (or alternatively apply $U^T$ to the bottom qubit). Second, replace the $R'_{xz}=UR_{xz}U^\dagger$ correction with the $R''_{xz}=U^TR_{xz}\overline{U}$ correction.
We know that $R'_{xz}\in\mathcal{C}^{(k-1)}$, but we don't know whether $R''_{xz}\in\mathcal{C}^{(k-1)}$. However, one of the changes to the protocol necessary to effect $U^T$ rather than $U$ is operationally very simple: apply $U$ on a different qubit. One might then suspect that the associated update to the correction isn't too complicated and in particular, the correction stays in $\mathcal{C}^{(k-1)}$. I don't know how to prove this at the moment, though. $\square$
Lemma 1 and Conjecture 3 combine to give us
Corollary 4 (Every level is closed under inversion)
For every $k\geqslant 1$, we have
$$U\in\mathcal{C}^{(k)}\iff U^\dagger\in\mathcal{C}^{(k)}\tag7.$$
