5

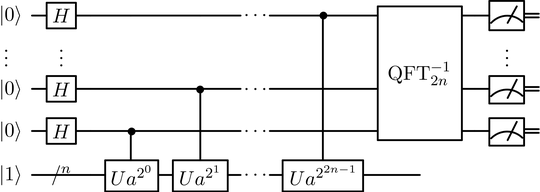
In the usual presentations (e.g. Nielsen and Chuang) Shor's algorithm (in its quantum part) is presented as a special case of phase estimation, meaning it uses a circuit of the form "generate superposition, apply function, apply $QFT^{-1}$, measure":

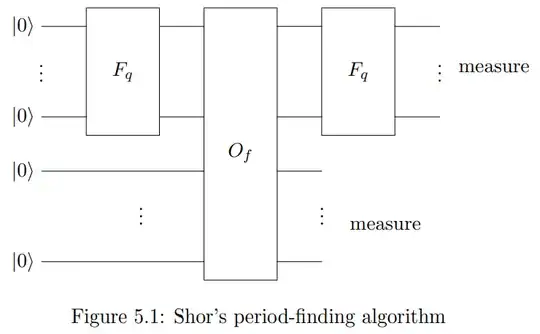
enter image description here

But when I try to look at Shor's algorithm as a (variation on a) special case of the Hidden Subgroup Problem, e.g. in de Wolf's lecture notes or this thesis, the circuit used is similar to the one for the general solution of the abelian HSP, which has $QFT$ and not $QFT^{-1}$ at the end:

enter image description here

The other parts of both algorithms seem the same to me, and I agree that in the general HSP algorithm one should use $QFT$ and not $QFT^{-1}$, so I wonder what's the source of the difference. Do both ways lead to the same good result, or is it something deeper?

Gadi A
  • 437
  • 2
  • 4

2 Answers2

6

$\text{QFT}\big(|0\rangle^{\otimes n}\big) = \text{QFT}^{-1}\big(|0\rangle^{\otimes n}\big) = |{+}\rangle^{\otimes n}$, so a QFT, inverse QFT, or a column of Hadamard gates are all equivalent at the beginning of the computation.

I feel that it's more morally correct to use $\text{QFT}$ at one end of the computation and $\text{QFT}^{-1}$ at the other, as the combinations $\text{QFT}\circ\text{QFT}$ and $H^{\otimes n}\circ\text{QFT}$ don't make sense mathematically, but in practice it doesn't matter. Also, it doesn't matter which one is on which end, as they differ only by complex conjugation, and the computation between them is classical (so equivalent to a permutation matrix, which is real).

benrg
  • 898
  • 5
  • 3
6

Note that $\text{QFT}^2$ is a permutation $|k\rangle \rightarrow |(-k) \bmod 2^n\rangle$. This is a classical operation. It can be applied in the post processing of the measurements, and in fact it can be applied cheaply.

Because the difference between $\text{QFT}^{-1}$ and $\text{QFT}$ is just "negate the index modulo a power of 2", and this is a cheap operation to apply classically, it doesn't matter which one you use at the end of the quantum part of phase estimation algorithms such as Shor's algorithm. Either one can be worked with by the later steps.

Actually, Shor's algorithm is basically insensitive to negating the quantum output. So even if the you screw up and use the $\text{QFT}^{-1}$ postprocessing but use the $\text{QFT}^{+1}$ circuit, it should still work.

Craig Gidney
  • 44,299
  • 1
  • 41
  • 116