How to perform the measurements on a quantum circuit in W state basis?

Question

I need to perform the measurements on a quantum circuit in the basis $\{ \eta^\pm,\zeta^\pm \} $. Where $ \eta^\pm,\zeta^\pm $ are given as follows: $$\eta^\pm = \frac{1}{2}|001\rangle + \frac{1}{2}|010\rangle \pm \frac{1}{\sqrt{2}}|100\rangle \\ \zeta^\pm = \frac{1}{2}|101\rangle + \frac{1}{2}|110\rangle \pm \frac{1}{\sqrt{2}}|000\rangle $$ How to obtain a mapping from any 4 of basis states ($|000\rangle,|001\rangle,\ldots |111\rangle$) to states $(\eta^\pm,\zeta^\pm)$? I was able to find the circuit and unitary for $\eta^\pm$ and $\zeta^\pm$ separately, but not a single unitary for mapping to all the four states.

The circuit $\eta^+$ with initial state $|000\rangle$ looks like:

Answer 1

You can easily verify that the four bases you have given, together with $|011\rangle$, $|111\rangle$, $(|001\rangle - |010\rangle)/\sqrt{2}$ and $(|101\rangle - |110\rangle)/\sqrt{2}$ together form a complete orthnormal basis.

You can now easily generate the matrix $U$ that converts from this basis to the standard computational basis by putting the 8 kets side-by side to form an 8x8 matrix. Since it is unitary, its inverse is $U^{-1} = U^{\dagger}$, which is just $U^T$ since this array has no imaginary components.

You can use the Qiskit UnitaryGate class to create a circuit that implements this matrix.

Answer 2

The answer by @FrankYellin already addresses how to find a unitary $U$ that performs the transformation from an orthonormal basis containing the four states $|\eta^{+}\rangle$, $|\eta^{-}\rangle$, $|\zeta^{+}\rangle$ and $|\zeta^{-}\rangle$ to the computational basis. Then to measure in such nontrivial basis one simply has to apply $U^{\dagger}$ before the usual measurements in the Z basis.

As for the determination of the actual quantum circuit for $U$, since this a $3$-qubit operation, it can be decomposed into a circuit with at most $20$ CNOTs via the optimized quantum Shannon decomposition. In fact, using a unitary of the form proposed by @FrankYellin,

\begin{equation} U = \begin{pmatrix} 0 & 0 & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & \frac{1}{\sqrt{2}} & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & -\frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{2} & \frac{1}{2} & 0 & 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & \frac{1}{2} & \frac{1}{2} & 0 & 0 & -\frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}, \end{equation}

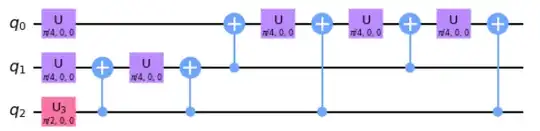
and qiskit.transpile in optimization_level=3 to do the basis gate decomposition, we find a circuit with $14$ CNOTs. However, we can find a shallower circuit by exploring the freedom to choose not only the computational basis states with which we associate the four reference states (i.e., to which columns of $U$ correspond $|\eta^{+}\rangle$, $|\eta^{-}\rangle$, $|\zeta^{+}\rangle$ and $|\zeta^{-}\rangle$) but also the additional four states we introduce to complete the basis. By conducting an exhaustive but not complete search over the multiple unitaries that arise from considering such variations, I have found the following circuit with $8$ CNOTs only.

OPENQASM 2.0;
include "qelib1.inc";
qreg q[3];
u3(0,1.2220253,-1.2220253) q[0];
u3(0,-0.5070985,-1.0636978) q[1];
u3(pi/8,-pi,-pi) q[2];
cx q[0],q[2];
u3(pi/8,0,0) q[2];
cx q[1],q[2];
u3(2.0712704,-pi/2,pi/2) q[1];
u3(pi/8,-pi,-pi) q[2];
cx q[0],q[2];
u3(pi/2,-pi,pi/2) q[0];
cx q[0],q[1];
u3(2.8566685,0,pi/2) q[0];
u3(pi/3,0.61547971,-2.5261129) q[1];
cx q[0],q[1];
u3(pi,-1.7561443,-1.4821301) q[0];
u3(pi/4,-pi,pi/2) q[1];
u3(0.85888576,2.1006991,1.2053066) q[2];
cx q[1],q[2];
u3(2.6302087,pi/2,-pi) q[1];
cx q[0],q[1];
u3(2.316649,0,pi/2) q[0];
u3(1.4093957,1.016652,-2.1249406) q[1];
cx q[0],q[1];
u3(pi/2,-pi/2,7*pi/8) q[0];
u3(7*pi/8,-pi,pi/2) q[1];
u3(pi/2,-pi/4,0) q[2]; 

This unitary $U$ associates $|\eta^{+}\rangle$ with $|100\rangle$, $|\eta^{-}\rangle$ with $|000\rangle$, $|\zeta^{+}\rangle$ with $|010\rangle$ and $|\zeta^{-}\rangle$ with $|110\rangle$.