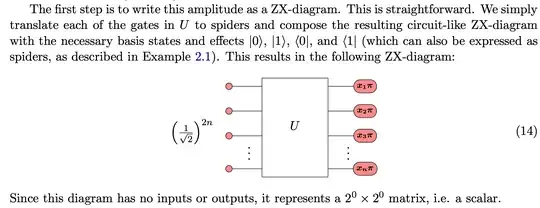
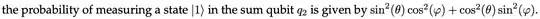OK, I made two mistakes. Both were corrected by a closer reading of the paper "Simulating quantum circuits with ZX-calculus reduced stabiliser decompositions".
First, as was pointed out by Craig, the leaf nodes didn't have the correct normalization. I needed to add factors of $\sqrt{2}$ for each computational basis state added. This is shown more clear in Eq 14 of the above paper, shown below.
Second, I incorrectly assumed that by putting computational basis leaf nodes to the graph, reducing them down to a scalar function would be equivalent to the probability. It is not. What's computed is the amplitude. So to get probability I just need to $|\cdot|^2$ it.
Alternatively, I can do like what they do in Eq 18 of the same paper and add the adjoint of the circuit. This seems unnecessary to me in most cases, unless you are wanting a marginal probability and don't want to enumerate over all possible cases.
That said, I figured enough out revisit the adder. Given the circuit:
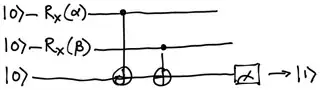
We can rewrite as a diagram
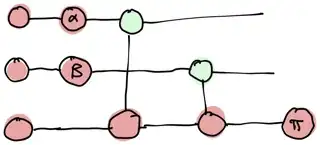
and then consider the probability of measuring the $|101\rangle$ state, that is, $P(x=|101\rangle)$.
We can augment with computational basis spiders, and be sure to extract the correct scalar value (6 computational basis states total, each with a $1/\sqrt{2}$ prefactor).
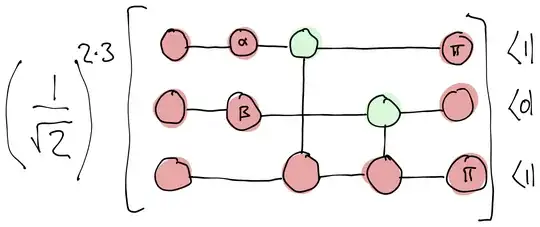
Finally, we can fuse:
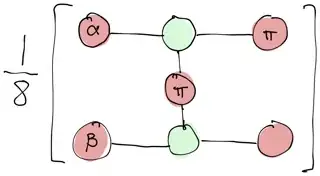
And then using the state copy rules get the scalar:
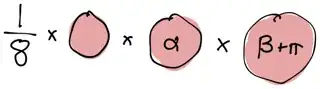
This evaluates to
$$
\frac{1}{8}\times 2 \times \left(1 + \exp{(i\alpha)}\right)\times \left( 1 + \exp{(i\left(\beta + \pi\right))}\right)
$$
or
$$
\frac{1}{4}\left(1 + \exp{(i\alpha)}\right)\times \left( 1 - \exp{(i\beta)}\right)
$$
such that
$$
P(x=|101\rangle) = \left|\frac{1}{4}\left(1 + \exp{(i\alpha)}\right)\left( 1 - \exp{(i\beta)}\right)\right|^2 = \cos^2{(\alpha/2)}\sin^2{(\beta/2)}
$$
as you can confirm here. The situation is analogous for the other non-zero contribution. Thus we obtain the result (Eq 7) in Widdows (2022).
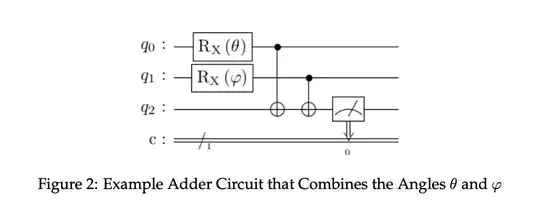
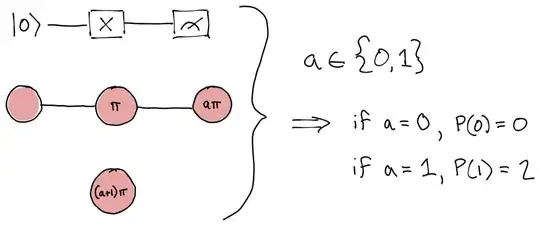Given the circuit above, I would expect to measure the qubit to be 
