Difference between min/max-entropies and the von Neumann entropy

Question

Consider the (smooth) min-entropy, max-entropy and von Neumann entropy of a given density operator $\rho_A$. Does a small gap between $H_{\max(\min)}(A)_\rho$ and $H(A)_\rho$ implies a small gap between $H_{\min(\max)}(A)_\rho$ and $H(A)_\rho$? Put in other words, does a small gap between the von Neumann entropy and either min- or max-entropy implies a nearly flat spectrum of $\rho_A$?

Answer 1

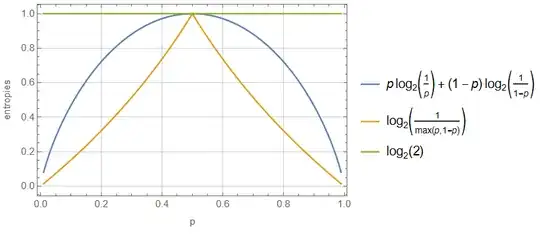
I'm not sure what you mean exactly with "small gap", but you can easily build examples where $H(A)$ and $H_{\rm max}(A)$ are "maximally different". For example, $$\rho = \begin{pmatrix}1-\epsilon & 0 \\ 0 &\epsilon\end{pmatrix}$$ for small $\epsilon>0$, has $H(\rho)\simeq 0$, but $H_{\rm max}(\rho)=\log|\operatorname{supp}(\rho)|=1$. You can build similar examples in any dimension. In these cases $H(\rho)\simeq H_{\rm min}(\rho)$ but $H_{\rm max}(\rho)$ is rather different.

On the other hand, to have $H(\rho)\simeq H_{\rm max}(\rho)$ it seems you'd need a more or less balanced nonzero eigenvalues, which would then also make $H_{\rm min}(\rho)\simeq H(\rho)$.

Here's a plot of the three quantities for the possible distributions over two outcomes:

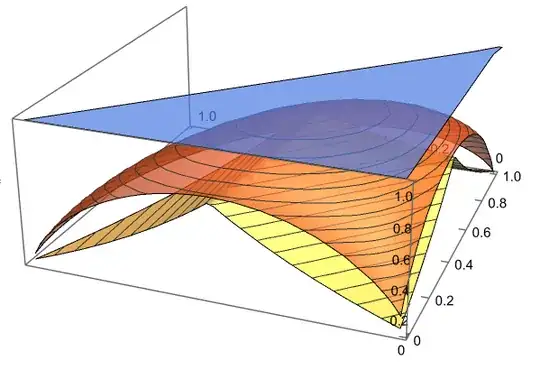
We can also do the same for three-outcome distributions, obtaining essentially the same result:

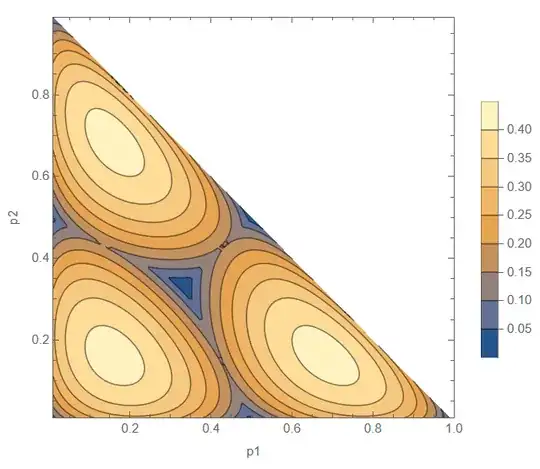
This is, however, significantly harder to parse without being able to rotate the figure. One way to see that the relations between $H,H_{\rm min},H_{\rm max}$ we had before remains here, is to show only the difference between $H$ and $H_{\rm min}$:

This clearly shows that $H\simeq H_{\rm max}$ whenever we have a balanced distribution, be it $P\simeq (1/3,1/3,1/3)$, or things like $P\simeq (1/2,1/2,0)$. But nearby this point, we also have $H\simeq H_{\rm min}$.