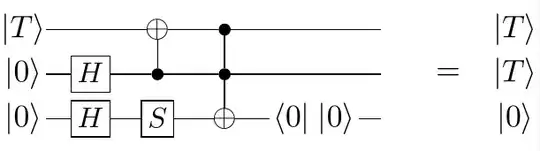
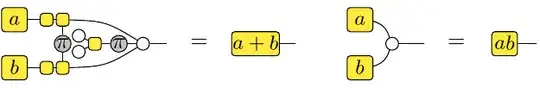$\newcommand{\ket}[1]{|#1\rangle}$Let us call some state $k$-qubit state $\ket{S}$ catalyzable by some other state $\ket{S'}$ if there is a Clifford+Toffoli circuit (possibly with ancilla and/or post-selection), that transforms $\ket{S} \otimes \ket{0}^{\otimes k} \otimes \ket{S'}$ to $\ket{S} \otimes \ket{S} \otimes \ket{S'}$. For instance, the $\ket{T}$ magic state is catalyzable by the state $\ket{0}$:
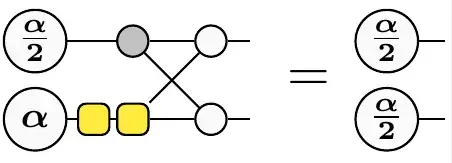
Note that the restriction to Clifford+Toffoli circuits is arbitrary, and we could also work with Clifford+T. From now on, I will use the ZH-calculus (a graphical calculus related to ZX-calculus) to express some identities as it yields more compact expressions - all the ZH-diagrams given here can in principle be translated to Clifford+Toffoli circuits with ancilla. The identity above is a special case of the fact that by consuming a $\ket{Z_\alpha} = \ket{0} + e^{i\alpha}\ket{1}$ state, we can transform $\ket{Z_{\alpha/2}}$ into $\ket{Z_{\alpha/2}}\otimes \ket{Z_{\alpha/2}}$:
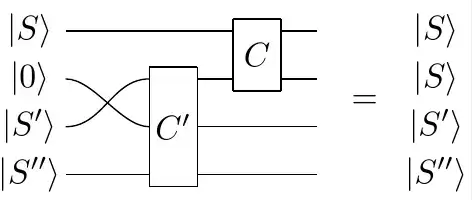
Since $\ket{T} = \ket{Z_{\pi/4}}$ and $\ket{Z_{\pi/2}} = SH\ket{0}$ can be prepared by a Clifford circuit, this can be used to 'bootstrap' the catalysis. These $\ket{Z_\alpha}$ states are significant because they can be used to create a $Z_\alpha$ phase-gate by magic state injection. Note that catalysis is kind of transitive - if $\ket{S} \otimes \ket{S'}$ can be transformed to $\ket{S} \otimes \ket{S}$ by a Clifford+Toffoli circuit $C$, and $\ket{S'}$ is catalyzed by $\ket{S''}$ with a circuit $C'$, then $\ket{S}$ can be catalyzed by $\ket{S'} \otimes \ket{S''}$:
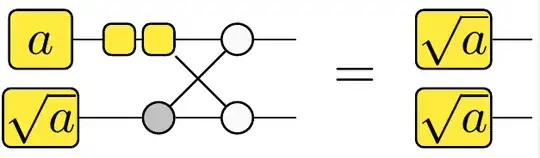
This implies that the states $\ket{Z_{\pi/ 2^k}}$ for $k > 2$ are also catalyzable, by the state $\ket{Z_{\pi/2^{k - 1}}} \otimes \cdots \otimes \ket{Z_{\pi/4}} \otimes \ket{0}$. In fact, we can generalize the construction that transforms $\ket{Z_{\alpha/2}} \otimes \ket{Z_\alpha}$ into $\ket{Z_{\alpha/2}} \otimes \ket{Z_{\alpha/2}}$ to operate on the unnormalized states $\ket{H_a} = \ket{0} + a\ket{1}$ (so $\ket{Z_\alpha} = \ket{H_{e^{i\alpha}}}$ - in ZH-calculus, these are H-boxes with one wire):
And so we can transform $\ket{H_\sqrt{a}} \otimes \ket{H_a}$ into $\ket{H_\sqrt{a}} \otimes \ket{H_\sqrt{a}}$. Using a Clifford+Toffoli circuit, we can also construct $\ket{H_{a + b}}$ and $\ket{H_{ab}}$ from $\ket{H_a}$ and $\ket{H_b}$:
Similar constructions exist for $\ket{H_{a - b}}$ and $\ket{H_{a / b}}$. We can also construct $\ket{H_k}$ directly for any $k \in \mathbb{N}$ (for example, see this paper by Backens et al), as well as $\ket{H_i} = SH\ket{0}$. This leads to the following result:
Theorem 1: $\ket{Z_\alpha}$ is catalyzable by some state $\ket{S}$ if $\alpha$ is an angle that can be constructed by straightedge and compass.
Proof: Since we can construct the integers, addition, multiplication, subtraction, and division with Clifford+Toffoli circuits, and square roots by introducing an extra catalyst qubit, any $a$ that can be constructed out of these operations starting from integers has $\ket{H_{a}}$ catalyzable. It is a famous result of Gauss and Wantzel that such numbers $a$ are exactly those such that the real and imaginary parts can be constructed by a straightedge and compass.
This means that quite a broad class of $\ket{Z_\alpha}$ are catalyzable, including $\ket{Z_{\pi/2^k}}$, $\ket{Z_{\pi/3}}$ (see this answer by Craig Gidney, for example), $\ket{Z_{\pi/5}}$, etc. Now we can, finally, get to my actual questions:
Question 1: Is the converse of Theorem 1 true, or are there non-constructible angles which are catalyzable? (The smallest possible counterexample would be $\frac{\pi}{7}$, but I haven't found anything in the literature about this)
Question 2: In general, if $\ket{Z_\alpha}$ is catalyzable, is $\ket{Z_{\alpha / 3}}$ also catalyzable? (This does not follow from the construction above because it is impossible to trisect a general angle with a straightedge and compass)
Question 3: What about other divisors, or even other functions of $\alpha$ - if $\ket{Z_\alpha}$ is catalyzable, for what $f : \mathbb{R} \to \mathbb{R}$ can $\ket{Z_{f(\alpha)}}$ be catalyzed?