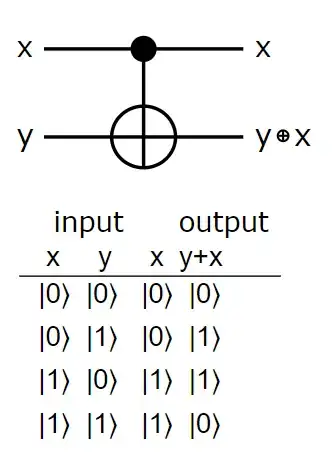1

I was reading about the Jordan gradient algorithm(https://arxiv.org/pdf/quant-ph/0405146.pdf) and I am a bit confused about one of the phrases:

Next, use the blackbox to compute f and add it modulo $N_0$ into the output register

For context, the Jordan gradient function calculates the gradient vector of a function or blackbox. The blackbox has an output of $N_0$ qubits

What exactly does

add it ..... into the output register

mean?

Thanks

MeltedStatementRecognizing
  • 145
  • 5

1 Answers1

2

If we understand what modular arithmetic is, I assume the question is how do we implement this in a quantum circuit?

Let's consider the simple 2-qubits case first (mod-2 addition):

The functionality of the $CNOT$ gate is writing the mod-2 addition product to the target qubit. Consider a quantum circuit with 2 qubits $q_o = x, q_1 = y$, then $CNOT(q_0,q_1)$ writes $q_1 = y \oplus x = y + x\ (mod\ 2)$:

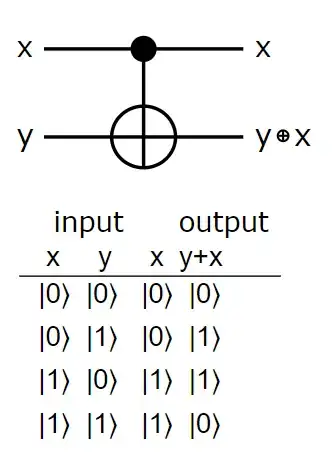
enter image description here

CNOT circuit diagram and truth table, from the CNOT wikipedia value.

Implementing mod-y addition:

Well, it's not that simple to implement mod-y addition (and adders in general) in a qunatum circuit. There are various methods to do that, and I am not sure there is a systematic method that can be applied for any arbitrary $y$ (Take a look at this QCSE post).

However, I like to get intuition for this by thinking about the operator being applied upon the target register in such mod-y addition. Ultimately, the operator being applied on the target register is not more than a permutation matrix. I will try to emphasize what I mean by taking an example of a target register consisted of $n = 2$ qubits and its statevector is $|\psi\rangle \in \mathbb{C}^{N = 4}$. Then "writing" some value $x\ (mod \ 4)$ to this register is equivalent to one of the following operators $U[x\ (mod\ 4)]$:

$$ U(0) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \ \ \ \ U(1) = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}$$

$$ U(2) = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \ \ \ \ U(3) = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{bmatrix}$$

Take a look at the matrices and understand how they permute the amplitudes of $|\psi\rangle$, which is essentially the modular addition operation. Those matrices are surely unitary so they can be implemented with quantum gates ($U(2)$ for example is fairly easy to implement with $X \otimes I$).

Edit - $x\ (mod\ y)$ permutation matrices:

I am adding this part as an answer to the questions in the comments. First, I would like to emphasize again that I have just proposed a method to get intuition for the general case of modular-addition, it helps me personally - Maybe it can help you as well. However for implementing an actual adder one needs to construct an adequate circuit.

However, regarding your question about the $3$ qubits case - What is the matrix representation for $x + 3\ (mod\ 5)$ - If $x$ is the value of the register than the following matrix operator is what you are looking for:

$$U_{3\ (mod\ 5)} = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}$$

I have wrote a little piece of code in Qiskit that generates modular addition operators that you can use for developing your intuition:

import numpy as np
import math
from qiskit.quantum_info import Operator

def generate_x_mod_y_AdditionOperators(x, y):
    N = 2 ** int(math.ceil(math.log(y, 2)))
    u = np.zeros(shape = (N,N))
    x_mod_y = x % y


permutation = 0
for i in range(x_mod_y, (y + x_mod_y)):
    u[i % y][permutation] = 1
    permutation += 1

for r in range(y,N):
    u[r][r] = 1

U = Operator(u)
return U

For example, this will return the exact operator $U_{3\ (mod\ 5)}$ that I have wrote above:

U = generate_x_mod_y_AdditionOperators(x = 3, y = 5)

You can also append this operator to a quantum circuit with any desired input, and then observe how the statevector is being affected by applying this operator.

Ohad
  • 1,899
  • 3
  • 15