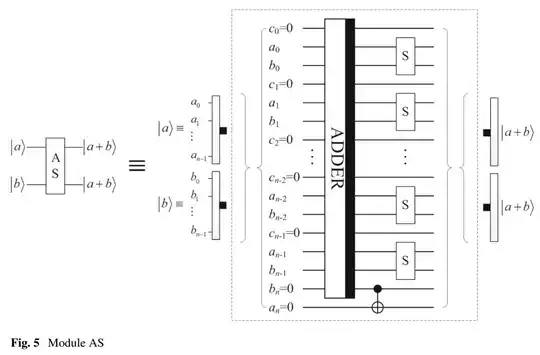
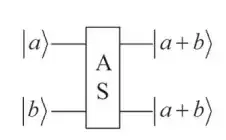
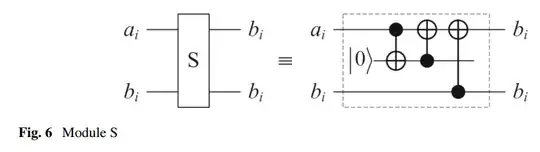
In Quantum adder of two states that are themselves superpositions, I asked:
I have two states $|a\rangle = \frac{1}{\sqrt N}\sum_{i=0}^{N-1}|i\rangle|a_i\rangle$ and $|b\rangle = \frac{1}{\sqrt N}\sum_{j=0}^ {N-1} |j\rangle|b_j\rangle$, with $i,j,a_i,b_j \in \mathbb{N}$.
I want to add $|a\rangle$ and $|b\rangle$ such that the output I get from an adder circuit is $|c\rangle = \frac{1}{\sqrt N}\sum_{i=0}^{N-1}|i\rangle|a_i+b_i\rangle$. Is this circuit possible?
One answer suggests 'no' to the question - but the journal article (and it's from International Journal of Theoretical Physics - reputable journal) suggests 'yes'. The problem is, the article does not seem to provide a real justification of the algorithm involved, thus the question. Here is the algorithm diagram of the gated article:
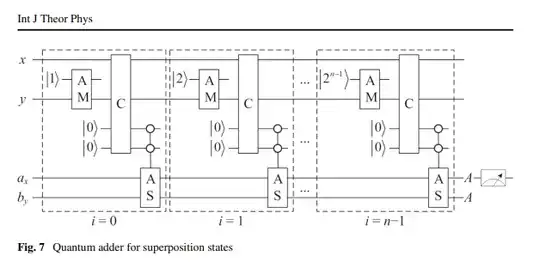
The article claims that given $|\psi\rangle = \frac{1}{2^n}\left[\sum_{x=0}^{2^n -1} |x\rangle|a_x\rangle\right]\left[\sum_{y=0}^{2^n -1} |y\rangle|a_y\rangle\right]$ and with $a_x = a_y$ when $x=y$, which makes $|\psi\rangle$ two identical non-entangled copies of the same state, one can compute $A = \sum_{i=0}^{2^n-1}a_i$ in $O(n)$, with the algorithm in the figure.
The AM module simply adds $|k\rangle$ to $|y\rangle$ modulo $2^n$ in the article and nothing more. The C module simply compares value of $|x\rangle$ and $|y\rangle$ and returns two qubits to be all $|0\rangle$ if they are equal. The AS module is a controlled module, which adds $|a_x\rangle$ and $|b_x\rangle$ only if comparator output bits are all $|0\rangle$. At stage $i$ of the figure, what happens is that $\frac{1}{\sqrt 2^n}\left[\sum_{x=0}^{2^n -1} |x\rangle|a_x\rangle\right]$ is summed with itself but along the same index $x$ as to produce $\frac{1}{\sqrt 2^n}\left[\sum_{x=0}^{2^n -1} |x\rangle|2 a_x\rangle\right]$. Which basically is the question I asked before.
For me, this adder does not seem to make any sense. Yet it comes from a reputable journal, and some articles have been using this algorithm. This makes me wonder what is going on.