First, I would like to state that I went through many excellent sources of information (among them - Grover's original paper, several QCSE posts like 1 2, and many more sources) - And yet I couldn't find a satisfying answer, so there must be something I don't understand.
I am trying to settle my mind with the known fact that Grover's algorithm can retrieve a specific value $w$ from an unsorted list in $O(\sqrt{N})$ steps, while $N$ is the size of the list. It is understood that $\frac{\pi}{4}\sqrt{N}$ iterations over Grover's iterator (Grover's oracle + diffuser operator) are needed, which may implies upon an overall computational complexity of $O(\sqrt{N})$.
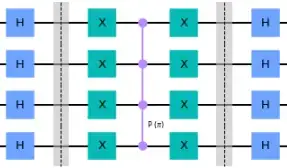
Grover's algorithm with n = 2, N = 4, one iteration over Grover's iterator.
But since Grover's orcale + diffuser are nested inside the iterator, as I understand it - We should be able to implement both of them independently of $N$, such that in each iteration both the oracle and the diffuser should contribute $O(1)$ steps to the overall complexity - If we want to achieve an overall complexity of $O(\sqrt{N})$.
There are several ways to implement the oracle and the diffuser, but as far as I understand - a multi-controlled gate over the $n = log(N)$ qubits in the counting register is unavoidable, in both:
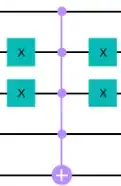
Implemention of the diffuser for n = 4 qubits with an mcz gate.
Implemention of the oracle for the $w = 1001$ with an mcx gate.
Decompositon of such multi-controlled gates would produce a circuit depth dependent of $n = log(N)$. So if in each iteration at least $O(log(N))$ steps being performed, then it seems to me that the overall complexity of the algorithm should be at least $O(\sqrt{N} \ log(N))$.
What am I missing? How is the overall complexity of $O(\sqrt{N})$ is being achieved after all?
Thanks!
